완전 이진 트리를 이해하기 위해
이진 트리에 대해서 알아보자.
이진 트리란?
위 그림은 이진트리의 가장 기본적인 구조이다. 부모는 자식을 갖는다. 이는 굉장한 의미를 갖는다. 버블정렬, 퀵정렬, 병합정렬은 모든 데이터가 동등한 지위를 갖었다. 그러나 힙정렬은 계층구조를 이용한다. 이런 수직적 구조는 '탐색'에 유용하기에 선택정렬을 응용한 힙정렬에는 알맞는 구조이다.
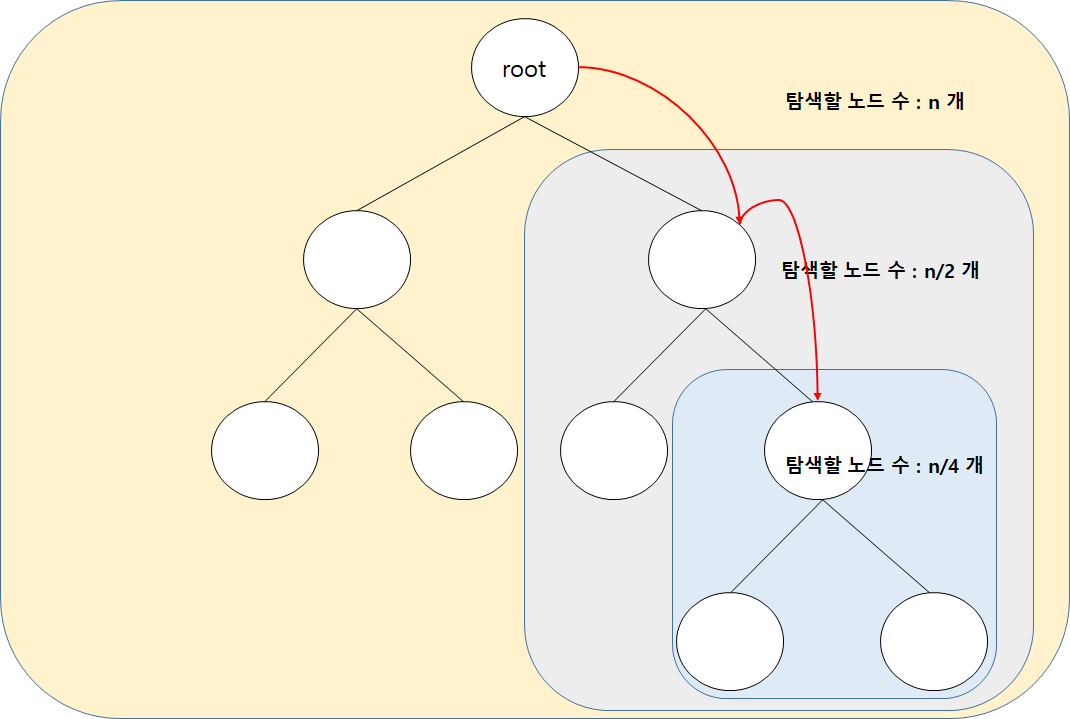
부모보다 작은 값은 왼쪽 자식, 부모보다 큰 값은 오른쪽 자식에 저장된다고 가정하자. 만약 탐색값이 부모보다 크다면 왼쪽 트리는 탐색할 필요가 없다. 그러므로 탐색할 노드의 수가 절반으로 줄어든다. 이와같이, 이진트리는 부모와 자식간의 규칙을 설정할 수 있다. 규칙은 데이터의 위치를 특정지을 수 있다. 이는 탐색에 유용하다.
그렇다면 구현은 어떻게 할까?
이진트리는 보통 '리스트(List)' 자료구조로 구현된다. 수정, 삽입, 삭제에 배열보다 유용하기 때문이다. 그러나 완전이진트리인 경우 배열도 유용하다.
완전이진트리는 좌측부터 빠짐없이 노드가 채워진 트리를 의미한다. 중간에 빈 부분이 많으면 배열이 낭비되는데 완전이진트리는 그런 부분이 없다. 단, 배열을 이용할거면 한 가지 주의해야 할 것이 있다.
배열에 계층의 개념이 주입되어야 한다. 한마디로 아무렇게나 값을 넣으면 안된다.
좌측 끝은 트리의 시작인 root가 차지한다. 그리고 그 다음은 root의 자식이 차지한다. 그리고 그 다음은 자식의 자식이 차지한다. 이렇듯 배열은 완전이진트리의 노드의 우선순위대로 채워져야한다. 그러므로 우리는 부모와 자식간의 인덱스 규칙을 잘 알아야 한다.
완전이진트리의 노드에 배열 인덱스를 부여해보았다.
부모가 0이면 왼쪽 자식은 1이다.
부모가 1이면 왼쪽 자식은 3이다.
부모가 2이면 왼쪽 자식은 7이다.
부모가 4이면 왼쪽 자식의 인덱스는 무엇일까?
부모가 N이면 왼쪽 자식은 2xN + 1이이고 오른쪽 자식은 2xN + 2 이다.
그러므로, 부모가 4이면 왼쪽 자식은 9이고 오른쪽 자식은 10이다.
완전이진트리의 규칙이 부모보다 작은 값은 왼쪽 자식, 부모보다 큰 값은 오른쪽 자식에 저장된다고 가정해보자. 탐색값이 부모보다 크다면 N ~ 2xN+1 까지의 인덱스는 탐색할 필요가 없다. 바로 2xN + 2부터 탐색을 시작하면 된다. 이처럼 완전이진트리는 배열로 구현하고 규칙성에 따라 탐색이 가능하다.
'알고리즘 > 자료구조' 카테고리의 다른 글
| [자료구조] 우선순위큐에 비교로직 전달하기 (0) | 2024.01.24 |
|---|---|
| [자료구조] HashMap 파헤치기 2 ( keySet(), values(), iterator() ) (0) | 2021.06.25 |
| [자료구조] HashMap 파헤치기 1 (Linked List + Red Black Tree) (5) | 2021.06.25 |
| [자료구조] 컬렉션 프레임워크 - List (0) | 2021.06.25 |