예제) 아래 이름 나열을 '가나다' 오름차순으로 나열하려고 할 때, 이름을 최소 몇 번 이동하면 구현이 가능할까?

위 이름 나열을 가나다 오름차순으로 나열하면 다음과 같다.

최소 횟수로 구현하려면 얼마나 공통된 순서로 배치되었는지를 확인하면 된다.
예를들어,
위치는 다르지만 류다영 → 신서리 → 이다영 → 홍원주 순은 두 배열 모두 동일하다. 그러므로 공통된 순서에 있지 않은 이름을 이동시키면된다.
[동적계획법] 최장공통문자열 ( Longest Common SubSequence )
동적계획법(Dynamic Programing)이란? 복잡하고 어려운 문제를 작은 단위로 '분할'한 후 다시 '결합'하여 최적의 답을 구하는 방법 동적계획법은 분할된 모든 경우의 수를 검토한다. 중복되는 경우
lordofkangs.tistory.com
두 문자열이 얼마나 공통된 순서로 배치되었는지를 파악하는 방법은 LCS 알고리즘 ( Longest Common SubSequnce)를 이용하면 된다.
목표 상태를 A,B,C.. 로 치환한다.

이를 기준으로 현재상태를 A,B,C...로 표현한다.

현재상태

목표상태

두 가지 상태의 LCS를 구한다.

LCS는 포인터A와 포인터B로 두 문자열을 비교한다.
경우는 크게 두 가지가 있다.
1) 두 포인터가 가리키는 문자가 동일한 경우
2) 두 포인터가 가리키는 문자가 동일하지 않은 경우
규칙)
동일하면 두 포인터를 모두 한 칸씩 이동한다.
동일하지 않으면 두 포인터 중 하나만 움직인다.
모든 경우의 수를 표현하기 위해 테이블을 만든다.
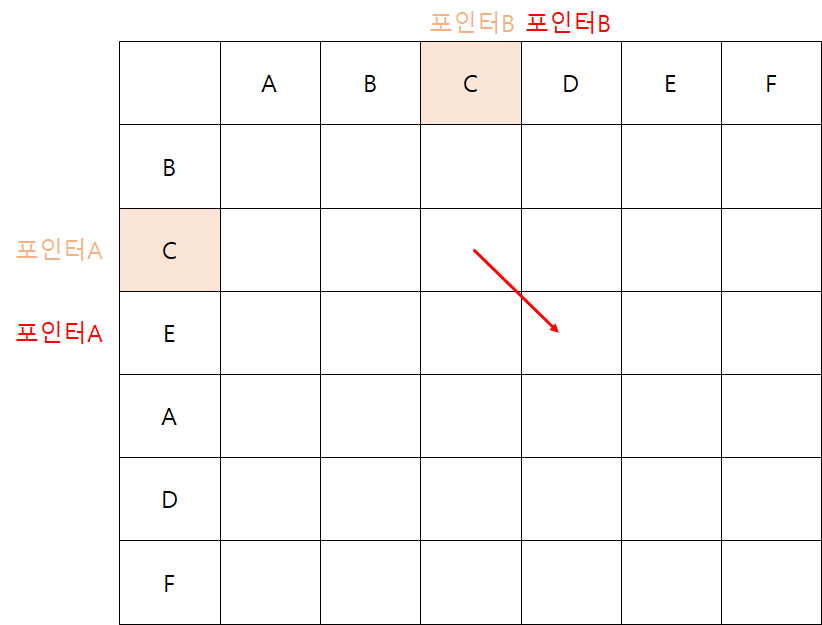
이렇게 포인터가 가리키는 문자가 동일하면 '대각선'으로 움직인다.
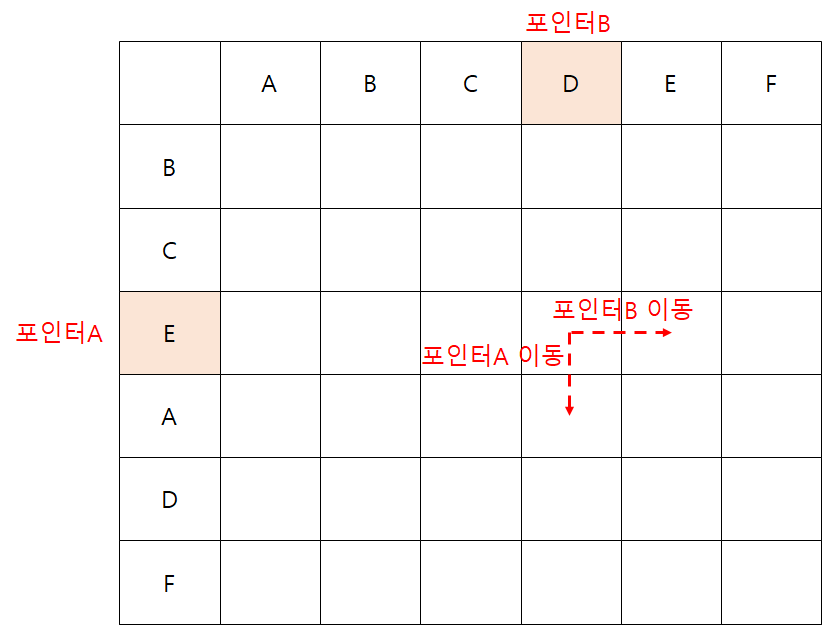
동일하지 않으면 수평이동 혹은 수직이동을 한다.

빈칸의 값은 머가 될까? 3가지 경우가 있다.
1) 포인터A, 포인터B 둘다 이동한 경우 ( 대각선 이동 )
2) 포인터A만 이동한 경우 ( 수직이동 )
3) 포인터B만 이동한 경우 ( 수평이동 )
1)은 아니다. 이전 대각선 방향의 문자인 A와 B는 동일하지 않기 때문이다.
그러므로 2)와 3) 두가지 경우만 가능하다. 우리가 구하는 경우는 Longest이다. 고로, 2)와 3) 중 Max 값을 선택한다.
?는 1이 된다.
이런 방식으로 테이블을 채워보자.

?는 무엇일까?
1) 포인터A, 포인터B 둘다 이동한 경우 ( 대각선 이동 )
2) 포인터A만 이동한 경우 ( 수직이동 )
3) 포인터B만 이동한 경우 ( 수평이동 )
이전 대각선 방향의 문자인 A와C는 다르다. 그러므로, 1)은 아니다.
2)나 3)이다. 둘 다 2이므로 Max는 2이다.
거기에 두 문자가 동일하므로 +1을 해주면 3이 된다.
?는 3이다.
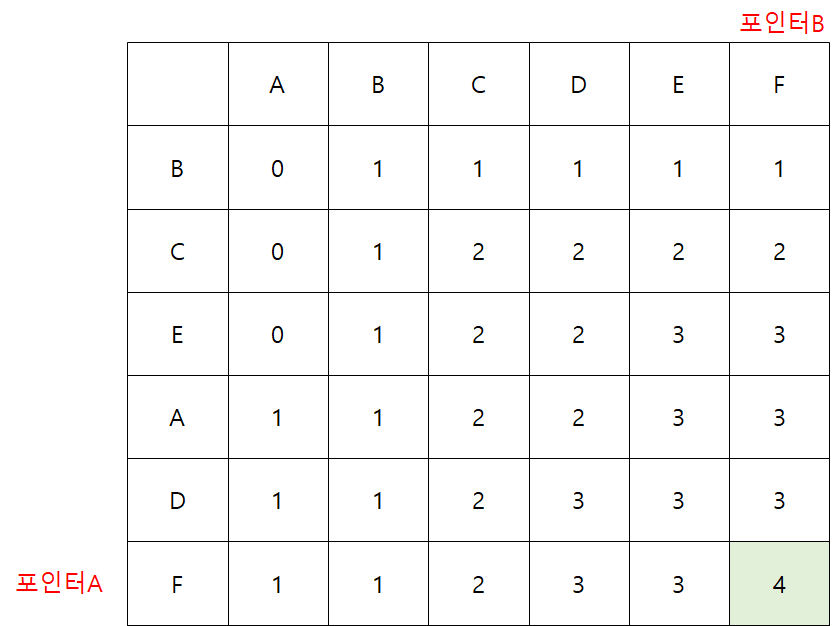
테이블을 완성하면 최종 LCS는 4가 된다.
현재상태

목표상태

현재상태와 목표상태 사이의 LCS는 4이다. 4개의 이름이 공통된 순서를 갖고 있다는 말이다.
고로, 2개의 이름만 움직이면 목표상태에 도달할 수 있다.
참고자료
2021년 7기 모집대비 SSAFY(삼성 청년 SW아카데미) SW적성진단 5일 완성
ㆍ객관식 이론 + 대표유형 + 유형 + 고난도 문항 수록ㆍ주관식 대표유형 + 유형 + 고난도 문항 수록ㆍ객관식 & 주관식 모의고사 수록ㆍ에세이(자소서) + 면접 자료 수록[무료제공]1. [합격시대] 객
book.naver.com
'문제풀이 > 알고리즘' 카테고리의 다른 글
| [최단경로] 모든 지점을 연결하는 길의 최소 길이 ( Minimun Spanning Tree ) (0) | 2021.11.10 |
|---|---|
| [Greedy] 하나의 문자로 통일하기 (0) | 2021.11.10 |
| [동적계획법] 두 문자열 비교하기 ( Longest Common SubString ) (0) | 2021.11.09 |
| [동적계획법] Longest Common SubSequence (0) | 2021.11.08 |
| [동적계획법] Longest Palindrome SubString (0) | 2021.11.07 |
