지도학습이란?
과거의 정보를 가지고 모델을 만들어, 현재 데이터를 기반으로 미래를 예측하는 패턴을 추출하는 학습방법이다.
( 번호판 인식, 날씨 예측, 시장 예측 )
지도학습에서 모델은 회귀 모델(Regression)이라 부른다.
'회귀'라는 단어는 어려우니,
그냥 단순히 입력값 X와 결과값 Y의 관계를 나타내는 모델이라 이해하면 된다.
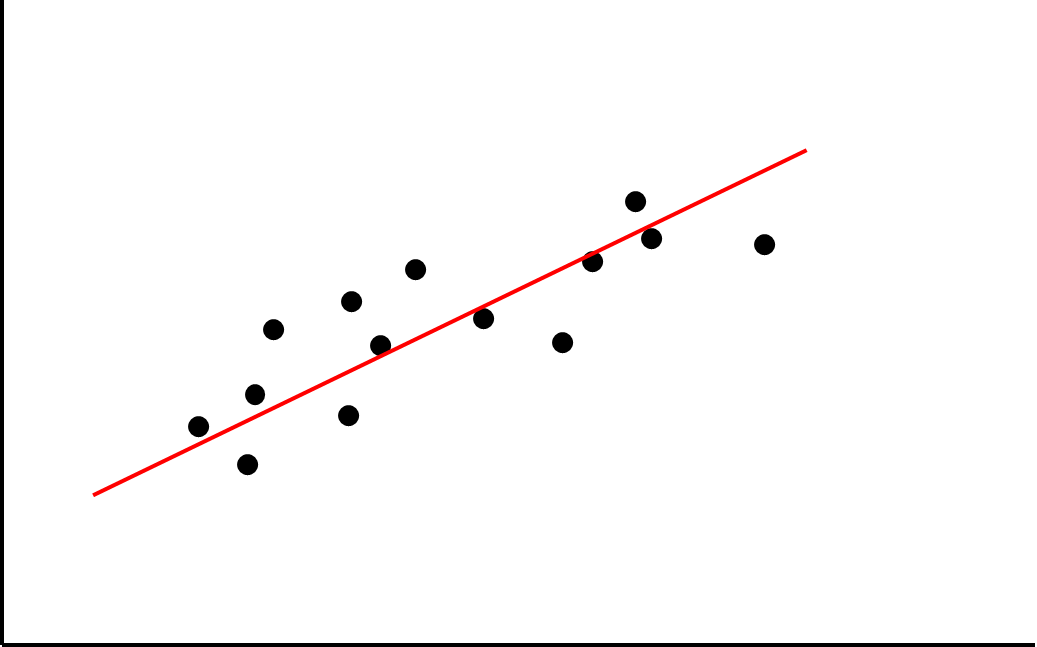
x와 y 좌표가 주어질 때, 이를 토대로 f(x)를 근사하는 것이 회귀(regresstion)이다. 회귀모델은 2차원 곡선에서 직선 혹은 곡선의 형태를 갖는다. 직선은 일차함수이고 곡선은 2차 이상의 고차함수이다.
선형회귀
선형회귀는 회귀모델이 1차 함수이다.
f(x) = mx + b
x에 따른 f(x)를 구하려면 기울기(m)과 절편(b)를 알아야 한다. 선형회귀는 m과 b를 찾는 문제이다. 기울기(m)를 가중치, 절편(b)을 바이어스(bias)라 부른다.
손실함수
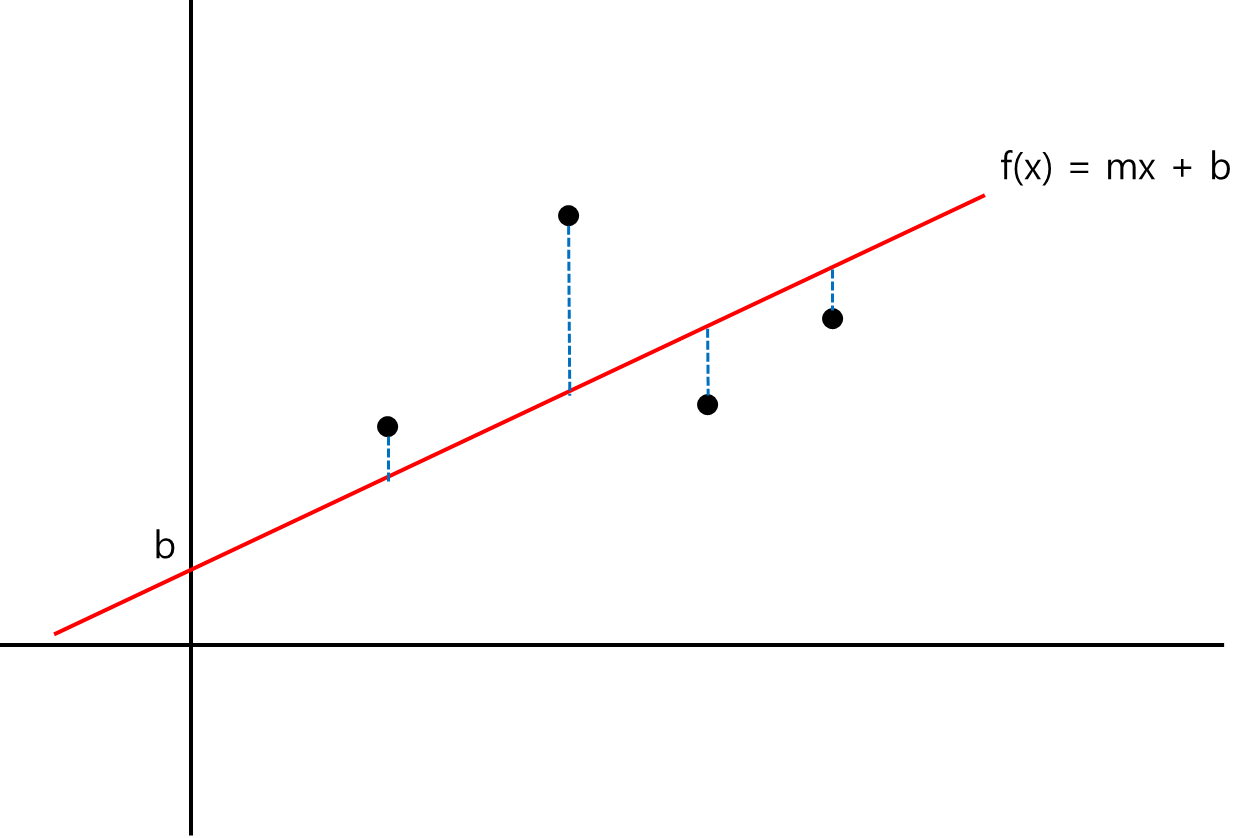
손실이란, 주어진 좌표 데이터와 회귀모델이 얼마나 멀리 떨어져있는가이다. 서로 가까이 있을수록 손실이 적다. 총 손실의 평균이 최소가 되는 회귀모델을 구해야한다. 이때, 손실은 f(xi) - yi가 된다. 기울기와 절편을 조정해가며 주어진 데이터와 손실이 최소가 되는 기울기와 절편을 찾아야 한다.
예를 들어보자.
기울기가 3이고 절편이 4이고 ( 2, 7 ), ( 3, 5 ), ( 5, 3 ) 세 좌표가 주어졌을 때 손실을 구해보자.
선형회귀 모델은 f(x) = 3x + 4가 된다.
x = 2 이면 f(x) = 10이 된다.
x = 3 이면 f(x) = 13이 된다.
x = 5 이면 f(x) = 19가 된다.
( 2, 7 ) : 손실은 | 10 - 7 | = 3 이다.
( 3, 5 ) : 손실은 | 13 - 5 | = 8 이다.
( 5, 3 ) : 손실은 | 19 - 3 | = 16 이다.
손실의 평균은 ( 3 + 8 + 16 ) / 3이 된다.

손실함수를 공식으로 표현한 것이다. 손실함수가 최소가 되는 지점을 구해야한다.
이때 '미분'이 사용된다.
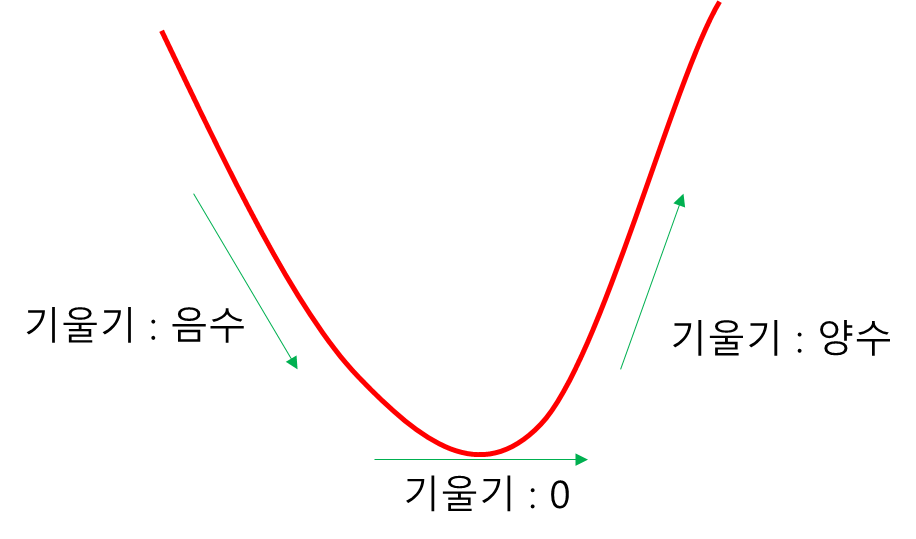
손실함수는 직선의 방정식을 제곱하여서 이차함수가 되었다. 미분을 하면 x지점의 기울기를 알 수 있다. 기울기가 음수에서 양수로 바뀌는 지점이 손실함수의 최소지점이다.
선형회귀의 경우, x의 종류가 하나이다.
현실은 무수히 많은 x(입력값)가 존재한다.
그래서 '편미분'을 사용해야한다.
이는 다음 포스팅에서 다루어보겠다.
'CS > 인공지능' 카테고리의 다른 글
| [인공지능] 기계학습 ( 분류기; Classifier ) (0) | 2021.12.13 |
|---|---|
| [인공지능] 기계학습 ( 경사하강알고리즘 ) (0) | 2021.12.13 |
| [인공지능] 기계학습 (0) | 2021.12.12 |
| [인공지능] 베이즈 정리 ( Bayes' theorem ) (0) | 2021.11.02 |
| [인공지능] 조건부 확률 (0) | 2021.11.01 |
