13549번: 숨바꼭질 3
수빈이는 동생과 숨바꼭질을 하고 있다. 수빈이는 현재 점 N(0 ≤ N ≤ 100,000)에 있고, 동생은 점 K(0 ≤ K ≤ 100,000)에 있다. 수빈이는 걷거나 순간이동을 할 수 있다. 만약, 수빈이의 위치가 X일 때
www.acmicpc.net
◎ 문제풀이
A지점에서 B지점으로 최소비용으로 이동하는 문제는 BFS로 풀어야 한다. 그러나 나는 최근에 DP 문제를 하나 풀어서 그런지, 이 문제를 보고 DP 발상을 했다. N에서 K까지 가는 경우를 모든 고려하는 문제이다.
이동하는 방법은 3가지이다.
1) x2
2) +1
3) -1
N이 5이고 K가 17이라고 가정해보자.
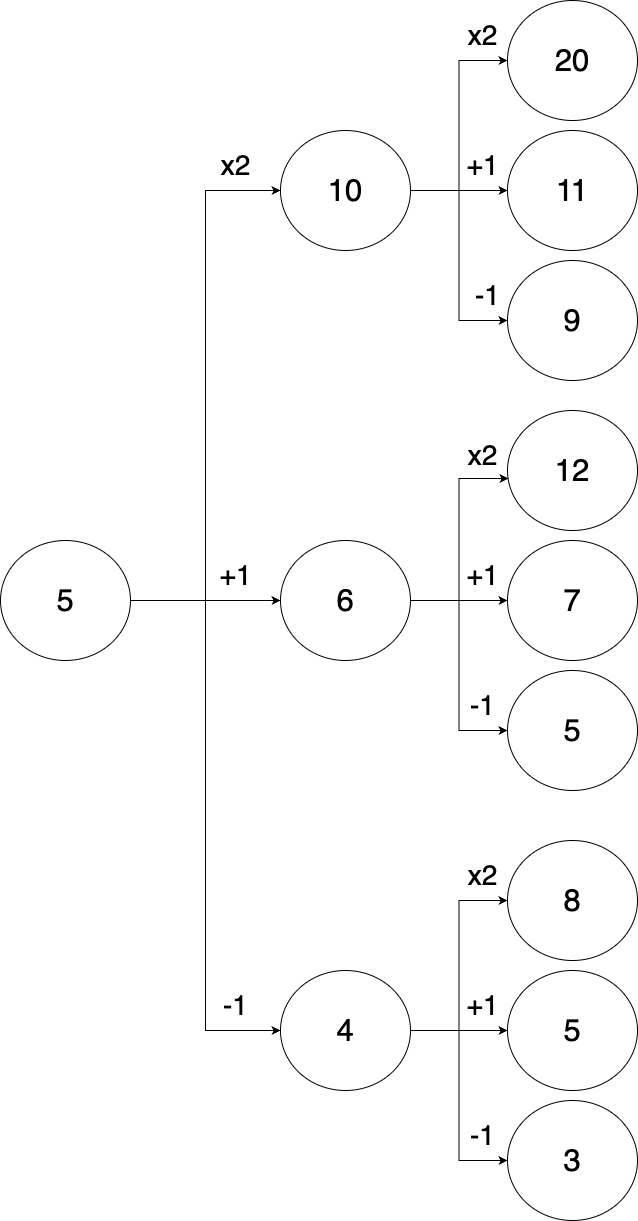
위 그림 같이, 경우의 수가 기하급수적으로 증가하니 DP로 풀기는 어려운 문제이다.
1) x2
2) +1
3) -1
3가지 경우가 주어졌다고 무조건 DP로 풀어야 한다는 식의 기계적인 풀이는 좋지 못하다.
A에서 B로 가는데 최소비용으로 가는 경우를 탐색해야 하므로 BFS로 풀어보자. 그런데 여기에는 한 가지 특별한 점이 있다. x2로 이동하는 경우에는 시간이 +1이 되지 않는다. 즉, 모든 이동의 가중치가 동일하지 않는 것이다. 다시말하여 BFS 탐색으로 먼저 도착해도 최소비용이 아닐 수 있다. '+1'로 3번 이동한 것보다 'x2'로 3번 이동한 후 '-1'로 다시 한번 이동하는 것이 비용이 더 적을 수 있다.
그러므로 K지점에 도착했다고 BFS탐색을 종료하면 안 된다. BFS 탐색으로 완전탐색을 하면서 K지점에 도착하는데 가장 적게 걸리는 시간을 찾아야 한다.
◎ 코드
import java.util.Arrays;
import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;
//BOJ13549 숨바꼭질3
public class Main {
public static final int MAX = 100000;
public static int[] time = new int[MAX+1]; // 시간 테이블
public static class Pos{
int index;
int time;
public Pos(int index, int time){
this.index = index;
this.time = time;
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int k = sc.nextInt();
Arrays.fill(time,Integer.MAX_VALUE);
bfs(n); // BFS 탐색으로 시간테이블 만들기
System.out.println(time[k]); // 출력
}
public static void bfs(int start){
Queue<Pos> queue = new LinkedList<>();
queue.add(new Pos(start,0));
time[start] = 0;
while(!queue.isEmpty()){
Pos curr = queue.remove();
// 시간테이블 입력된 시간보다 작은 경우만 큐에 넣는다.
// x2
if(2*curr.index < MAX+1 && curr.time < time[2*curr.index]) {
queue.add(new Pos(2*curr.index,curr.time));
time[2*curr.index] = curr.time;
}
// +1
if(curr.index+1 < MAX+1 && curr.time+1 < time[curr.index+1] ) {
queue.add(new Pos(curr.index+1,curr.time+1));
time[curr.index+1] = curr.time+1;
}
// -1
if(curr.index - 1 >= 0 && curr.time+1 < time[curr.index-1]) {
queue.add(new Pos(curr.index-1,curr.time+1));
time[curr.index-1] = curr.time+1;
}
}
}
}'문제풀이' 카테고리의 다른 글
| [PS] BOJ1967 트리의 지름 ( tree + dfs ) with JAVA (0) | 2023.08.31 |
|---|---|
| [PS] BOJ15486 퇴사2 ( dp ) with JAVA (0) | 2023.08.30 |
| [PS] BOJ2608 로마숫자 ( string ) with JAVA (0) | 2023.08.28 |
| [PS] BOJ14675 단절점과 단절선 ( tree ) with JAVA (0) | 2023.08.28 |
| [PS] BOJ1068 트리 ( tree ) with JAVA (0) | 2023.08.25 |
