11066번: 파일 합치기
소설가인 김대전은 소설을 여러 장(chapter)으로 나누어 쓰는데, 각 장은 각각 다른 파일에 저장하곤 한다. 소설의 모든 장을 쓰고 나서는 각 장이 쓰여진 파일을 합쳐서 최종적으로 소설의 완성본
www.acmicpc.net
◎ 문제풀이
아직까지는 하나의 알고리즘 문제에 다른 알고리즘이 응용되는 문제를 푸는게 쉽지 않은 것 같다. '파일 합치기' 문제도 DP 알고리즘에 누적합 알고리즘을 적용해야 풀리는 문제이다.
파일은 최종적으로 두개의 묶음으로 합쳐진다. dp[i][j]가 i부터 j까지 묶음의 최대값이라고 해보자.

> dp[1][5] = dp[1][1] + dp[2][5] + C1 ~ C5까지의 합
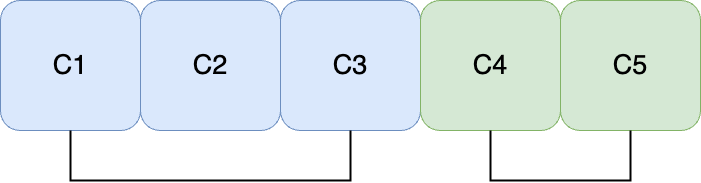
> dp[1][5] = dp[1][3] + dp[4][5] + C1 ~ C5까지의 합

> dp[1][5] = dp[1][2] + dp[3][5] + C1 ~ C5까지의 합
등등 여러 가지 경우가 존재한다.
끝에 'C1 ~ C5까지의 합'을 더해주는 이유는 최종적으로는 모든 파일을 합치는 비용을 합해야 한다고 문제에 나와 있기 때문이다. C1 ~ C5까지의 합은 누적합 알고리즘을 이용한 구간합으로 구한다. 이해를 돕기 위해 아래 예를 들어보자.

> dp[1][5] = dp[1][3] + dp[4][5] + C1 ~ C5까지의 합(구간합 )
dp[1][5]를 구하려면 dp[1][3]이 메모리제이션 되어 있어야 한다. dp[1][3] 또한 두개의 묶음이 합쳐진 것이다.
> dp[1][3] = dp[1][1] + dp[2][3] + C1~C3까지의 합( 구간합 )
◎ 코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
//BOJ11066 파일 합치기
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int t = Integer.parseInt(br.readLine());
while(t-- >0){
int ans = 0;
int n = Integer.parseInt(br.readLine());
int[] sum = new int[n+1];
int[][] dp = new int[n+1][n+1];
StringTokenizer st = new StringTokenizer(br.readLine());
for(int i=1;i<=n;i++){
int file = Integer.parseInt(st.nextToken());
sum[i] = sum[i-1] + file; // 누적합
}
// DP테이블 만들기
for(int i=1;i<=n;i++){ // 1부터 n까지 DP테이블 만들기
for(int from=1; from+i<=n; from++ ){ // from-to 묶음별 최댓값 구하기
int to = from+i;
dp[from][to] = Integer.MAX_VALUE;
for(int mid=from;mid<to;mid++){ // from-mid , mid+1-to 두개 묶음으로 최댓값 구하기
dp[from][to] = Math.min(dp[from][to],dp[from][mid] + dp[mid+1][to] + sum[to] - sum[from-1]);
}
}
}
System.out.println(dp[1][n]);
}
}
}'문제풀이 > DP' 카테고리의 다른 글
| [PS] BOJ17484 진우의 달 여행 ( DP ) with JAVA (0) | 2024.01.27 |
|---|---|
| [PS] BOJ15989 1,2,3 더하기4 ( dp ) with JAVA (0) | 2023.10.18 |
| [PS] BOJ1520 내리막 길 ( DP + DFS ) with JAVA (0) | 2023.09.11 |
| [PS] BOJ15486 퇴사2 ( dp ) with JAVA (0) | 2023.08.30 |
| [PS] BOJ2655 가장높은탑쌓기 ( dp ) with JAVA (0) | 2023.08.21 |