11729번: 하노이 탑 이동 순서
세 개의 장대가 있고 첫 번째 장대에는 반경이 서로 다른 n개의 원판이 쌓여 있다. 각 원판은 반경이 큰 순서대로 쌓여있다. 이제 수도승들이 다음 규칙에 따라 첫 번째 장대에서 세 번째 장대로
www.acmicpc.net
1. 문제 추상화
원판 개수에 따른 하노이탑 최소 이동 횟수와 이동 과정을 출력하시오.
2. 알고리즘
▷ 하노이탑 개념
수학적 사고력이 뛰어나거나 하노이탑의 개념을 어느정도 알아야 풀 수 있는 어려운 문제이다. 나 또한 하노이탑에 대해서 잘 모르기에 여기저기 찾아보며 풀었다.
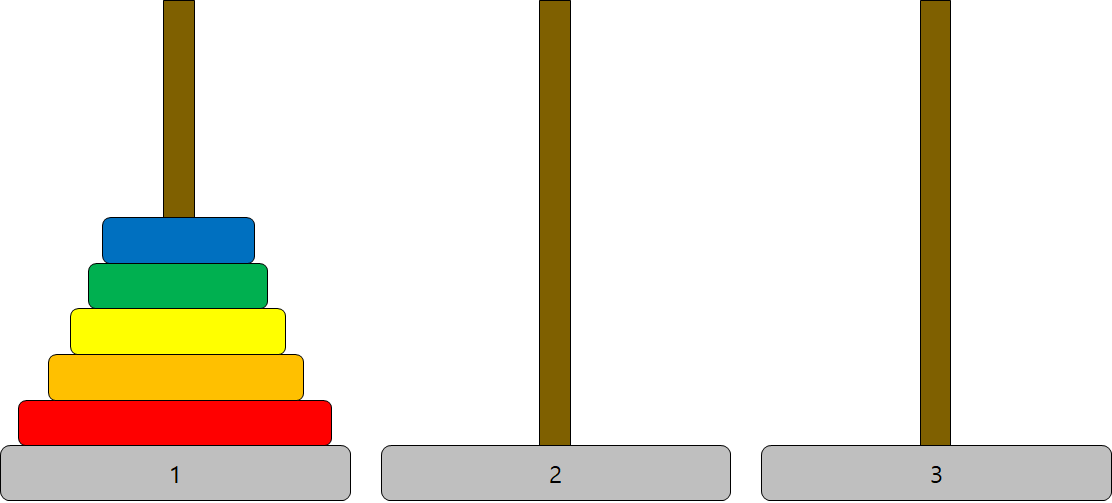
1번에 쌓여있는 원판들을 3번까지 옮겨야 한다. 단, 규칙이 있다.
1. 1회에 한 개의 원판만 옮길 수 있다.
2. 반드시 큰 원판 위에 작은 원판이 있어야 한다.
재귀적 사고를 하려면 처음부터 차례대로 생각하는 선형적 사고를 버려야한다. 결과부터 생각해보자.

1번에 있는 원판들을 모두 3번까지 옮기려면 우선적으로 가장 큰 빨간색 원판이 '3번'에 자리잡아야 한다. 이를 위해, 나머지 원판들은 2번에 차곡차곡 쌓여있어야 한다. 그래야 1번에서 3번으로 빨간색 원판을 옮길 수 있다.

그럼 이제 2번에 쌓여있는 원판들을 3번으로 옮기면 된다. 빨간색 원판은 이미 옮겨졌으니 제외하자. 그러면 가장 큰 원판은 주황색 원판이 된다. 주황색 원판을 2번에서 3번으로 옮기려 한다. 그렇다면 나머지 원판들은 1번에 차곡차곡 쌓여있어야 한다. 그래야 2번에서 3번으로 주황색 원판을 옮길 수 있다.

주황색 원판을 3번으로 옮기면 그림과 같이 된다. 이를 토대로 알고리즘을 만들어보자.
▷ 알고리즘
'옮긴다.' 라는 말 안에는 규칙이 포함되어 있다.
1. 1회에 한 개의 원판만 옮길 수 있다.
2. 반드시 큰 원판 위에 작은 원판이 있어야 한다.
이 규칙을 F라고 부르겠다.
옮겨야 하는 원판 수 : n
원판이 쌓여 있는 곳 : Start
원판의 옮겨야 하는 곳 : End
나머지 원판의 임시로 쌓아 놓는 곳 : Middle
- F(n) : 규칙 F 에 따라 원판 N개를 Start에서 End로 옮기시오.
- 알고리즘
1) 가장 큰 원판을 제외한 나머지 원판을 Middle로 옮긴다. ( n - 1 개 )
2) 가장 큰 원판을 Start에서 End로 옮긴다. ( 1개 )
3) 나머지 원판을 Middle에서 End로 옮긴다. ( n - 1 개 )
'옮긴다'에는 규칙 F가 적용된다. 그러므로 이를 기호로 표시해보자.
1) F ( n - 1 ) ( Start -> Middle ) 총 원판 이동 횟수 : S(n-1)
2) F ( 1 ) ( Start -> End ) 총 원판 이동 횟수 : 1
3) F ( n - 1 ) ( Middle - > End ) 총 원판 이동 횟수 : S(n-1)
원판이 n개인 경우, 총 원판 이동 횟수 : S(n) = 2*S(n-1) + 1
이것이 하노이탑이 대표적 재귀함수 풀이인 이유다. 선형적으로 1부터 2,3,4... 하나씩 규칙을 적용할 생각이면 '반복문'이 효과적이다. 그러나 하노이탑처럼 내가 원하는 지점부터 역순으로 규칙을 적용하는 경우 '재귀함수'가 효과적이다.
3. 코드
1. 총 원판의 이동 횟수 출력
2. 원판의 이동 경로 출력
package boj11729;
import java.util.Scanner;
public class Main {
private static StringBuilder sb = new StringBuilder();
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt(); // 원판의 개수 : n
sb.append(countHanoi(n)).append("\n");// 총 원판 이동 횟수 출력
hanoi(n,1,2,3); // F(n) ( 1 (Start) -> 3 (End) ) 원판 이동 경로 출력
System.out.println(sb.toString());
}
// 재귀함수 : 원판 이동 경로 출력
public static void hanoi(int n, int start, int middle, int end) {
if(n==1) {
sb.append(start+" "+end).append("\n");
return;
}
hanoi(n-1,start,end,middle); // F(N-1) ( Start -> Middle )
sb.append(start+ " " +end).append("\n"); // F(1) ( Start -> End )
hanoi(n-1,middle,start,end); // F(N-1) ( Middle -> End )
}
// 재귀 함수 : 총 원판 이동 횟수 출력
public static int countHanoi(int n) {
if(n==1) {
return 1;
}else {
return 2*countHanoi(n-1)+1;
}
}
}
'문제풀이' 카테고리의 다른 글
| [JAVA] 백준 2798번 블랙잭 : 브루트포스 (0) | 2021.07.28 |
|---|---|
| [JAVA] 백준 2447번 별찍기-10 : 재귀함수 (0) | 2021.07.27 |
| [JAVA] 백준 3053번 택시 기하학 : 유추 (0) | 2021.07.24 |
| [JAVA] 백준 1002번 터렛 : 두 원의 교차점 (0) | 2021.07.24 |
| [JAVA] 백준 3009 네 번째 점 : Simple is best (0) | 2021.07.23 |
