2447번: 별 찍기 - 10
재귀적인 패턴으로 별을 찍어 보자. N이 3의 거듭제곱(3, 9, 27, ...)이라고 할 때, 크기 N의 패턴은 N×N 정사각형 모양이다. 크기 3의 패턴은 가운데에 공백이 있고, 가운데를 제외한 모든 칸에 별이
www.acmicpc.net
1. 문제 추상화
입력된 값 N은 3의 거듭제곱이다. 만약 N이 3이면 출력은 아래와 같다.

N이 3보다 클 경우, 크기 N의 패턴은 공백으로 채워진 가운데의 (N/3)×(N/3) 정사각형을 크기 N/3의 패턴으로 둘러싼 형태로 출력하시오.
2. 알고리즘
어려운 문제다. 문제를 이해하기 힘들어서 인터넷을 찾아봐서 풀었다. 그래도 이번 문제를 통해 재귀함수를 깊이 이해할 수 있었다.
재귀적 사고와 선형적 사고는 다르다.

선형적 사고는 1부터 N까지 순서대로 특정 패턴(F)을 적용하는 방식이다. 보통 반복문을 통해 구현된다. 선형적 사고는 탐색에 유용하다. 패턴에 어떤 N을 입력해야 원하는 결과가 나오는지 탐색하기 위해, N을 선형적으로 증가시킨다.

재귀적 사고는 '목표 N'이 이미 주어져있다. N이 적용된 패턴의 결과, 즉 F(N) 도출이 목적이다. 그러나 패턴(F)는 일반적인 함수가 아니다. X를 입력한다고 Y가 나오지 않는다. F(N)을 알려면 F(N-1)도 알아야 한다. 이렇게 N부터 1까지 역순으로 패턴을 적용시킨 후 다시 되돌아와 F(N)의 값을 파악하는 방식이 재귀적 사고이다. 이는 재귀함수로 구현된다.
▷ 알고리즘
해당 문제는 패턴과 목표 N이 주어진다. 패턴 N은 N/3의 패턴을 답습한다. 그러므로 이는 재귀함수로 구현해야한다.
패턴 : 크기 N의 패턴은 공백으로 채워진 가운데의 (N/3)×(N/3) 정사각형을 크기 N/3의 패턴으로 둘러싼 형태
목표 : 입력받은 3의 거듭제곱 값
우선, 패턴을 이해해보자.
N = 27

N = 27이면 N/3은 9이다. 그러므로 F(27) 패턴은 9 X 9 정사각형 공백을 F(9) 패턴의 정사각형으로 둘러싸는 형태이다.
이를 추상화해보자.

F(N) 패턴을 아홉 개의 구역으로 나누면 4구역이 공백이고 나머지 구간은 F(N/3) 패턴이 적용된다. 그러므로 4구역을 제외한 나머지 구간에서 재귀함수를 호출하면 된다. 간략히 코드로 표현하면 아래와 같다.
for(int i=0; i<9; i++) {
if(i != 4) { // 4구역을 제외한 나머지 구간은 N/3 재귀함수 호출
F(N/3);
}else {
// 4구역은 공백
}
}
이러다 N=3이 되면

위 패턴을 구현해야 한다.
▷ 구현 방법

이같이 복잡한 패턴의 *을 찍으려면 이차원 배열을 이용해야 한다. 구역마다 재귀함수로 패턴이 적용되니 이차원 배열의 구역 구분을 확실히 해주어야 한다.
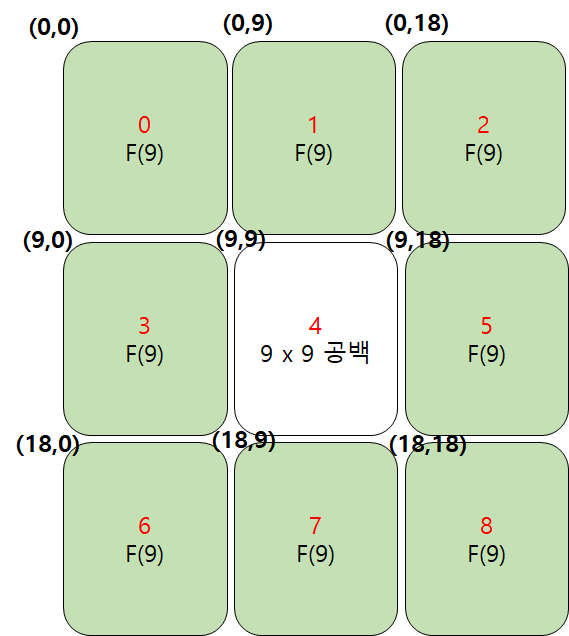
N이 27이면 27*27 정사각형이므로 arr[27][27] 이차원 배열이 만들어진다. 아홉 개의 구역의 시작점의 인덱스는 위 그림과 같다. i는 0~9 구역을 의미하고 (x,y)에서 x가 행, y가 열을 의미할때 좌표는 아래와 같다.
x = (N/3) * ( i / 3 )
y = (N/3) * ( i % 3 )
EX)
▷ i = 2 ( 2 구역 )
x = 0
y = 18
▷ i = 8 ( 8 구역 )
x = 18
y = 18
그리고 F[27]의 2구역의 시작점은 F[9] 패턴의 시작점이 되고 F[9]의 2구역은 F[3]의 시작점이 된다. 그러므로 재귀함수 호출시 매개변수로 각 구역의 시작점이 되는 인덱스를 실인수로 넣어준다.
// 재귀함수
public static void pattern(int n, int coordX, int coordY) { //coordX와 coordY는 각 구역의 시작점
if(n==3) { //n이 3인 경우
for(int i=0; i<9; i++) {
if(i!=4) { // 4구역이 아닌 경우, 1 저장
arr[coordX+i/3][coordY+n/3*i%3] = 1;
}else { // 4구역인 경우, 0 저장
arr[coordX+i/3][coordY+n/3*i%3] = 0;
}
}
return;
}
// n이 3보다 큰 경우
for(int i=0; i<9; i++) {
if(i != 4) { // 4구역이 아닌 경우, 재귀함수 호출
pattern( n/3, coordX + n/3*(i/3), coordY + n/3*(i%3));
}else { // 4구역인 경우, 공백 채우기
fillEmpty(n/3, coordX + n/3*(i/3), coordY + n/3*(i%3));
}
}
}
이렇게 아홉 개의 구역을 나누고 다시 재귀함수를 호출하여 또 나누고 나누고 하여 N=3이 될때, 이차원 배열을 1과 0으로 채우면 arr[27][27]은 모두 1과 0으로 채워진다. 이차원 배열에 값이 모두 저장되면 1과 0에 따라 문자와 공백을 출력해주면 된다.
3. 코드
import java.util.Scanner;
public class Main {
public static int[][] arr;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
arr = new int[n][n]; // 이차원 배열 생성
pattern(n,0,0); // 재귀함수 호출
StringBuilder sb = new StringBuilder();
for(int i=0; i<arr.length;i++) {
for(int j=0; j<arr[i].length; j++) {
if(arr[i][j] == 1) {
sb.append("*"); // 1인 경우, * 출력
}else {
sb.append(" "); // 0인 경우, 공백 출력
}
}
sb.append("\n");
}
System.out.println(sb.toString());
}
// 재귀함수
public static void pattern(int n, int coordX, int coordY) {
if(n==3) { //n이 3인 경우
for(int i=0; i<9; i++) {
if(i!=4) { // 4구역이 아닌 경우, 1 저장
arr[coordX+i/3][coordY+n/3*i%3] = 1;
}else { // 4구역인 경우, 0 저장
arr[coordX+i/3][coordY+n/3*i%3] = 0;
}
}
return;
}
// n이 3보다 큰 경우
for(int i=0; i<9; i++) {
if(i != 4) { // 4구역이 아닌 경우, 재귀함수 호출
pattern( n/3, coordX + n/3*(i/3), coordY + n/3*(i%3));
}else { // 4구역인 경우, 공백 채우기
fillEmpty(n/3, coordX + n/3*(i/3), coordY + n/3*(i%3));
}
}
}
// 4 구역 공백 채우기
public static void fillEmpty(int n,int coordX, int coordY) {
for(int i=0; i<n; i++) {
for(int j=0; j<n; j++) {
arr[coordX+i][coordY+j] = 0;
}
}
}
}'문제풀이' 카테고리의 다른 글
| [JAVA] 백준 18870번 좌표압축 : HashMap (임의접근) (0) | 2021.09.12 |
|---|---|
| [JAVA] 백준 1018번 체스판 다시 칠하기 : 정반대 경우의 수 (0) | 2021.07.29 |
| [JAVA] 백준 11729번 하노이 탑 이동 순서 : 재귀함수 (0) | 2021.07.26 |
| [JAVA] 백준 3053번 택시 기하학 : 유추 (0) | 2021.07.24 |
| [JAVA] 백준 1002번 터렛 : 두 원의 교차점 (0) | 2021.07.24 |