인공지능에게 게임이란?
게임은 추상적으로 정의가능하며 비교적 적은 연산자를 가진다.
게임의 인공지능 구현은 지적 능력과 관련있다고 여겨진다.
게임 조건
- 경기자는 두 명
- 제로썸 게임 ( 승자와 패자가 나뉨 )
- 차례대로 수를 둠
MiniMax 알고리즘
경기자는 최상의 수를 선택한다는 가정 하에 결과를 예측하는 알고리즘이다.
- 경기자
Max : 항상 큰 값을 선택한다.
Min : 항상 작은 값을 선택한다.
- 알고리즘
1) 경우의 수 펼치기 ( Top-down )
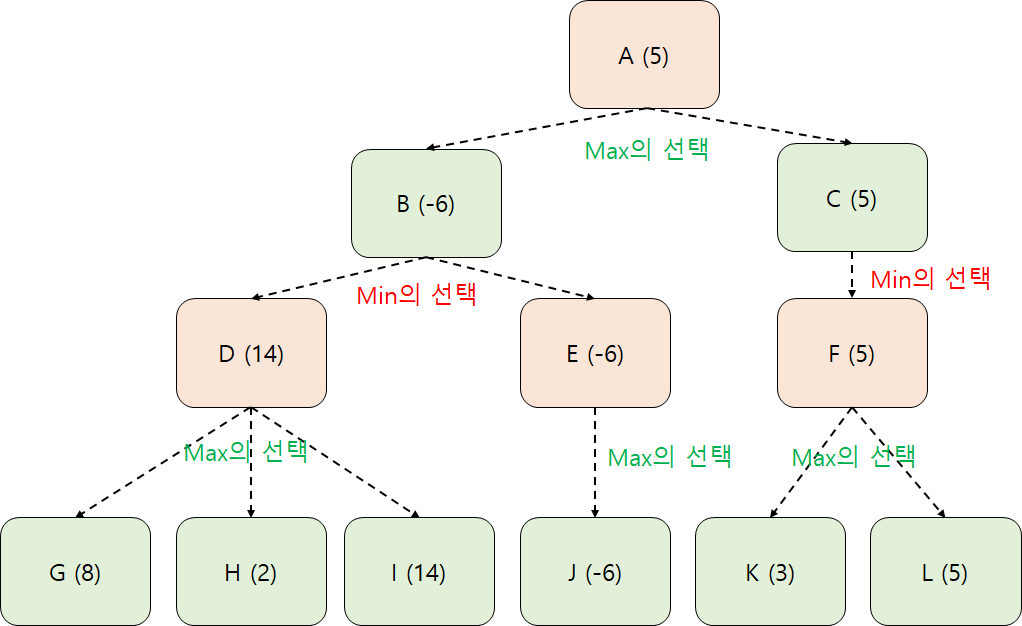
위 그림은 depth가 4인 게임트리이다. 게임 참여자가 둘 수 있는 경우를 모두 노드로 표현한다. 그리고 상대가 최적의 수를 둔다는 판단하에 게임결과를 예측하는 것이다. A 경우부터 보자.
A 경우에서 Max는 B 경우와 C 경우를 선택할 수 있다. ( 이제부터 '경우'를 생략하겠다. )
B에서 Min은 D와 E를 선택할 수 있다.
D에서 Max는 G와 H와 I를 선택할 수 있다.
이런 방식으로 모든 경우의 수를 살펴보면 위 그림 같은 게임트리가 완성된다. 이제 게임이 어떻게 흘러갈지 예측해보자.
2) 예측값 부여하기 ( Bottom-up )
단말 노드는 '게임의 결과'를 의미한다. 게임의 결과를 수치로 표현한 것을 휴리스틱 값이라 부른다. 그러므로 결과부터 올라가면서 각 경우에 예측할 수 있는 결과(휴리스틱 값)를 부여해야한다.
Max는 G와 H와 I 경우 중 하나를 선택해야한다.
G는 8이다. H는 2이다. I는 14이다.
그러므로 D 경우는 Max가 최선의 선택을 한다는 가정 하에, 결과(휴리스틱값)가 14로 예측된다.
Min은 D와 E 경우 중 하나를 선택해야한다.
D는 14이고 E는 -6이다.
그러므로 B 경우는 Min이 최선의 선택을 한다는 가정 하에, 결과(휴리스틱값)가 -6으로 예측된다.
이런 방식으로 모든 경우의 예측 결과값을 위 그림 같이 부여할 수 있다. 휴리스틱 값이 모두 부여되면 결과를 예측할 수 있다. A 경우의 예측 결과값은 5이다. 게임 참여자가 최적의 수를 선택한다는 가정 하에 A → C → F → L 로 흘러갈 것임을 예측했다.
Tic-Tac-Toe 게임
Tic-Tac-Toe 게임은 3X3 격자에 동일한 무늬로 직선을 완성하면 승리하는 게임이다. 9개의 격자가 있으므로 총 경우의 수는 9! ( 362,880 가지 ) 이다.
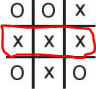
-MiniMax 알고리즘 적용하기
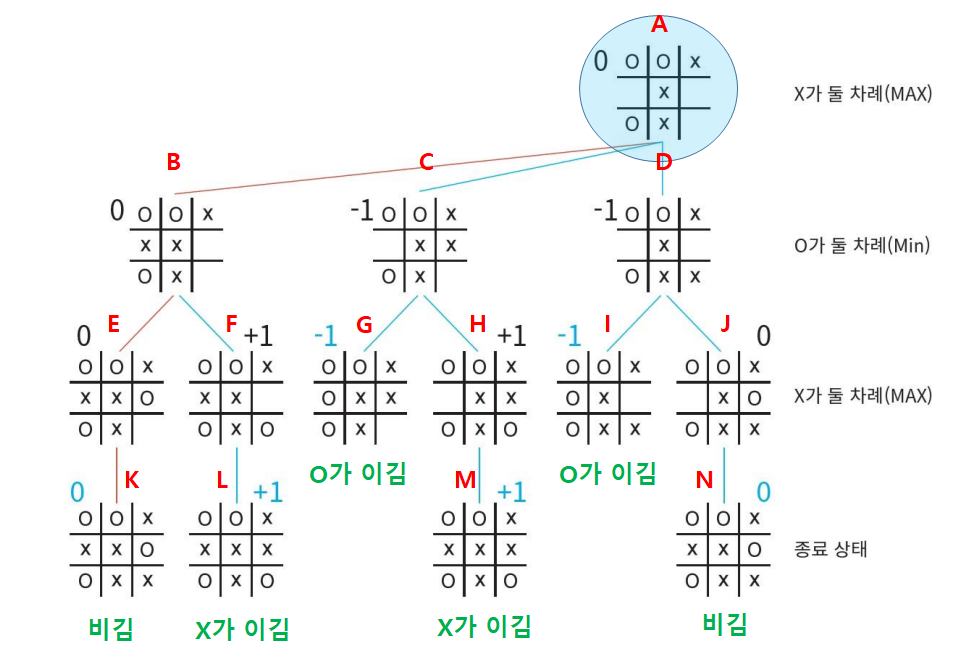
Max는 X이고 Min은 O이다.
A 경우에서 X는 B, C , D 경우를 선택할 수 있다.
B 경우에서 O는 E, F 경우를 선택할 수 있다.
이런 방식으로 모든 경우의 수를 탐색하면 위 게임트리가 완성된다.
결과를 예측해보자.
Max(X)가 이기는 휴리스틱 값은 +1이다.
Min(O)이 이기는 휴리스틱 값은 -1이다.
서로 비기는 휴리스틱 값은 0이다.
K 경우는 비기는 경우라 0이다.
L 경우는 X가 이기는 경우라 +1이다.
E 경우에서 Max(X)는 K밖에 선택권이 없으므로 예측결과값은 0이다.
B 경우에서 Min(O)은 E(0)와 F(+1) 경우 중 최소 비겨야하므로 예측결과값은 0이다.
이렇게 예측 결과값을 부여하면 위 게임트리처럼 완성된다.
Min(O)이 A라는 수를 둔다면 0이라는 예측결과값을 갖는다. 서로 최선의 선택을 한다는 가정 하에, 게임은 A → B → E → K 로 흘러갈 것이기 때문이다. 고로, Min(O)이 A라는 수를 두면 이길 수가 없다는 결론이 나온다.
정리하면.
MiniMax 알고리즘은
상대가 최선의 선택을 한다는 가정 하에
모든 경우의 수를 탐색하여
예측결과값를 추출하는 알고리즘이다.
'CS > 인공지능' 카테고리의 다른 글
| [인공지능] 전문가시스템 (0) | 2021.10.29 |
|---|---|
| [인공지능] 게임트리 ( 알파베타 가지치기 ) (3) | 2021.10.27 |
| [인공지능] A* 알고리즘 (0) | 2021.10.25 |
| [인공지능] 언덕 등반 기법 (Hill-Climbing) (0) | 2021.10.24 |
| [인공지능] 넓이 우선 탐색 ( BFS; Breadth First Search ) (0) | 2021.10.24 |