[인공지능] 게임트리 ( MiniMax 알고리즘 )
인공지능에게 게임이란? 게임은 추상적으로 정의가능하며 비교적 적은 연산자를 가진다. 게임의 인공지능 구현은 지적 능력과 관련있다고 여겨진다. 게임 조건 - 경기자는 두 명 - 제로썸 게임 (
lordofkangs.tistory.com
지난 포스팅에서 MiniMax 알고리즘을 다루었다. MiniMax 알고리즘은 게임트리의 모든 노드를 탐색하여 결과를 예측한다. 그러나 모든 노드를 탐색할 필요는 없다. 게임트리의 노드는 동적으로 생성되기에 적절한 조건문을 부여하면 필요없는 탐색을 줄일 수 있다.
이를 구현한 알고리즘이 알파-베타 가지치기(Alpha-Beta Pruning)이다.
알파-베타 가지치기(Alpha-Beta Pruning)
알파-베타 가지치기는 MiniMax 알고리즘을 보완한 알고리즘이므로 MiniMax 알고리즘부터 간략히 알아보겠다.
* MiniMax 알고리즘
경기자는 최상의 수를 선택한다는 가정 하에 결과를 예측하는 알고리즘이다.
- 경기자
Max : 항상 큰 값을 선택한다.
Min : 항상 작은 값을 선택한다.
Max와 Min은 늘 최상의 수를 선택하므로 모든 노드를 탐색할 필요가 없다. 알파베타 알고리즘은 α, β 변수를 이용하여 쓸데 없는 탐색을 줄인다. α는 Max가 어떤 선택을 할지 예측한 값, β는 Min이 어떤 선택을 할지 예측한 값을 나타낸다. 고로 자식노드들은 α, β 변수를 공유한다.
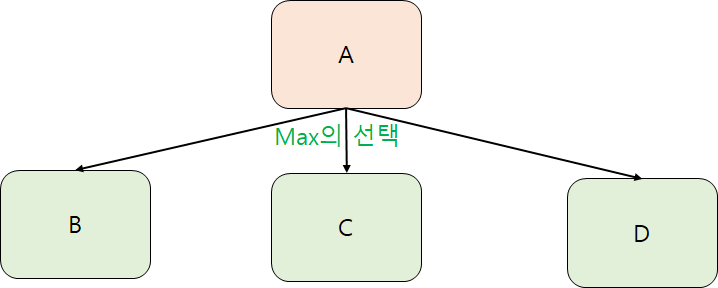
탐색을 줄이는 원리는 간단하다. Max가 선택할 수 있는 경우의 수는 3가지이다. B, C, D 노드 중 하나를 선택할 수 있다. B 노드를 탐색하면 B노드의 값을 알 수 있다. B노드 값이 7이라 해보자. 그럼 α값은 7이 된다. 이제 C와 D 노드를 탐색해야한다. 이때, C와 D의 α값이 7보다 크지 않을 것이라 예상된다면 탐색을 중단하여 쓸데없는 탐색비용을 줄인다. 어차피 Max는 가장 큰 값을 선택하기 때문이다.
그럼 좀 더 자세히 들어가보자.
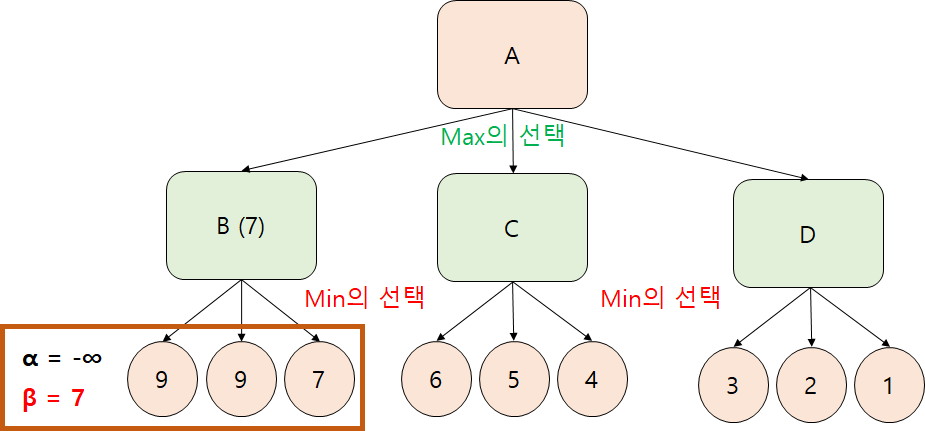
B 노드는 자식노드를 3개 갖고 있다. 이는 Min이 선택해야 할 경우들이다. Min은 항상 작은 값을 선택하므로 7을 선택한다. 고로 β는 7이 된다. 7은 B노드의 값이 된다.

탐색은 B노드까지 이루어졌다. B 노드의 값이 7이므로 Max가 어떤 선택할지 나타내는 예측값인 α는 7이 된다. 이제 C노드를 탐색해보자. 만약 C 노드의 α가 7보다 작을 것이라 예측되면 더 이상의 탐색은 무의미하므로 D 노드로 탐색이 넘어간다.

부모노드 세계에서는 Max가 선택권이 있으므로 α가 큰 값이 선택받는다. C 노드는 α값을 넘겨줘 자식노드들이 β값과 비교하도록 한다. β가 α보다 작으면 탐색이 무의미해지기 때문이다. 자식노드는 좌측부터 내림차순으로 정렬되어 있다. 맨 좌측값이 부모로부터 받은 α보다 작으면 나머지 자식노드는 탐색이 쓸모 없어진다. 자식노드의 β값이 곧 C노드의 α값이 되지만 7보다 작으므로 Max의 선택을 받지 못한다. 고로, 탐색을 중단하고 '가지치기'한다. (Pruning)

D 노드도 마찬가지이다. D노드의 맨 좌측값이 7보다 작은 3이므로 더 이상의 탐색은 무의미하다.
α, β 변수는 Max와 Min이 어떤 선택을 할지 예측한 값이 들어간다. Max가 B 노드를 선택하면 Min이 7을 선택하므로 α는 7이된다. C와 D노드의 α가 7보다 크지 않으면 자식노드를 탐색할 필요없이 가지치기한다. MiniMax처럼 모든 경우의 수를 탐색하지 않고 필요한 노드만 탐색하는 방식이 바로, 알파-베타 가지치기 알고리즘이다.
'CS > 인공지능' 카테고리의 다른 글
| [인공지능] 지식표현방법 ( 의미망, 프레임 ) (0) | 2021.10.30 |
|---|---|
| [인공지능] 전문가시스템 (0) | 2021.10.29 |
| [인공지능] 게임트리 ( MiniMax 알고리즘 ) (0) | 2021.10.26 |
| [인공지능] A* 알고리즘 (0) | 2021.10.25 |
| [인공지능] 언덕 등반 기법 (Hill-Climbing) (0) | 2021.10.24 |
