동적계획법(Dynamic Programing)이란?
복잡하고 어려운 문제를 작은 단위로 '분할'한 후 다시 '결합'하여 최적의 답을 구하는 방법
동적계획법은 분할된 모든 경우의 수를 검토한다.
중복되는 경우의 검토 비용을 줄이기 위해 기존의 결과를 저장한다.
최소 동전 개수 ( Min Coin Change )
동전 2원, 3원 5원이 있다. 각 동전은 무수히 많이 존재한다. 합이 11원이 되는 최소 동전 개수를 구하라.
Top-Down
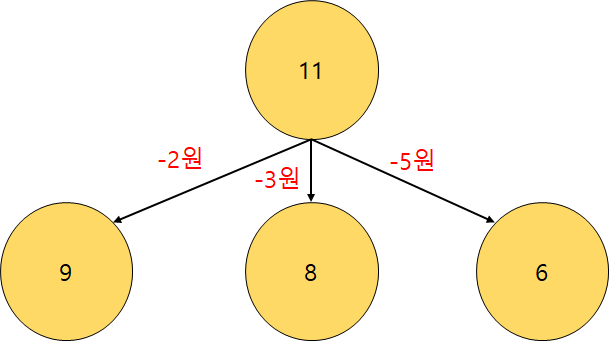
11원은 3가지 경우로 분할된다. 3가지 경우의 동전 개수 중 최소를 구해야 한다. 그럼 분할을 계속해보자.

4원은 3가지 경우가 있다.
2원 + 2원
1원 + 3원
-1원 + 5원
각 가격 별 최소 동전 개수의 배열은 아래와 같다.

1원 이나 음수인 경우 -1을 삽입하여 제외시키도록 하자
2원 ( 1개 )
1원 ( -1개 )
-1원 ( -1개 )

4원은 2원 + 2원이 되어 2개가 된다. 이런 방식으로 최소 동전 개수를 배열 안에 저장시키면 중복값 계산을 피할 수 있다.

위 계층에 있는 4원은 아래 계층에서 이미 계산되어 배열에 저장되어 있으므로 더 이상 계산하지 않아도 된다. 꼭대기(Top) 부터 내려가면서 분할과 결합을 반복하면 11원일 때, 최소 동전 개수를 구할 수 있다.
Bottom-Up
Top-Down 방식은 보통 재귀함수로 구현된다. 재귀함수는 같은 함수를 반복적으로 호출하는 방식이다. 함수는 영역(local)을 갖는다. 그래서 많이 호출되면 그만큼 스택메모리를 잡아먹는다. 엄청나게 큰 수를 구하고 싶으면 그만큼 많은 함수가 호출되므로 스택오버플로우가 발생할 수 있다. Bottom-Up 방식은 반복문을 이용하여 큰 값도 구할 수 있다.
11원부터 분할하지 말고 가장 작은 단위인 2원, 3원, 5원부터 하나씩 배열을 채워나가보자.

4원에서 2원, 3원, 5원을 뺀 뒤 최소 개수를 구해보자.
F(4) = MIN ( F(2), F(1), F(-1) ) + 1
F(1)과 F(-1)은 -1이므로 제외한다. F(2)를 MIN으로 선택한다.
F(4) = 2

F(6) = MIN ( F(4), F(3), F(1) ) + 1
F(1)은 -1이니 제외한다.F(4)는 2이다.F(3)은 1이다.고로, F(3)을 선택한다.
F(6) = F(3) + 1 = 1 + 1 = 2

이와 같은 방식으로 하나씩 배열을 채워나가면 11원을 구할 수 있다.
참고자료
'알고리즘 > 알고리즘' 카테고리의 다른 글
| [동적계획법] Maximum Sum SubArray (0) | 2021.11.07 |
|---|---|
| [동적계획법] Decoding Ways (0) | 2021.11.05 |
| [동적계획법] 최소 경로 비용 합 ( Minimum Path Sum ) (0) | 2021.11.05 |
| [동적계획법] 최소비용 계단 오르기 ( Min Cost Climbing Stairs ) (0) | 2021.11.04 |
| [동적계획법] 피보나치 수열 (0) | 2021.11.04 |