동적계획법(Dynamic Programing)이란?
복잡하고 어려운 문제를 작은 단위로 '분할'한 후 다시 '결합'하여 최적의 답을 구하는 방법
동적계획법은 분할된 모든 경우의 수를 검토한다.
중복되는 경우의 검토 비용을 줄이기 위해 기존의 결과를 저장한다.
Maximum Sum SubArray
예제) 정수로 구성된 한 수열이 주어질 때, 합이 최대가 되는 부분수열을 구하라.
[ 5, -2, 9, -15, 8 ]
동적계획법을 발상하기 어려운 문제다.
부분수열로 분할 할 수 있는 경우의 수가 너무 많다. Top에서 Down하면서 분할하기가 쉽지 않다. 그래서 일반적으로는 브루트 포스 방법을 생각하게 된다.
[ 5 ] , [ 5 ,-2 ] , [ 5, -2, 9 ] , [ 5, -2, 9, -15 ] , [ 5, -2, 9, -15, 8 ]
[ -2 ], [ -2 , 9 ] , [ -2 , 9 , -15 ] , [ -2 , 9 , -15, 8 ]
[ 9 ], [ 9, -15 ], [ 9, -15, 8 ]
[ - 15 ], [ -15 , 8 ]
[ 8 ]
이중 for문을 사용하여 위 경우를 모두 조사할 수 있다.
브루트 포스를 사용하지 않아도 동적계획법의 BottomUp 방식을 사용하면 모든 경우의 수를 고려한 최적의 값을 구할 수 있다.
Bottom-Up
1) [ 5 ]

부분수열로 한 가지 경우가 있다. 최대 Sum은 5이다.
2) [ 5 , -2 ]

부분수열로 2가지 경우가 있다. 최대 Sum은 3이다. ( 부분수열 [ 5 ]도 존재하지만 이전 단계에서 처리했으니 제외한다. )
3) [ 5, -2, 9 ]

부분수열로 3가지 경우가 있다. 최대 Sum은 12이다.
패턴은 간단하다.
[ 5 , -2 ]일 때, [ -2 ] 와 [ 5 , -2 ]이었으니
[ 5, -2, 9 ]이면 [ 9 ] , [ -2, 9 ] 그리고 [ 5, -2, 9 ]가 된다.
[ 9 ] , [ -2, 9 ], [ 5, -2, 9 ] 중 최대 Sum을 구해야 한다.
[ -2, 9 ]와 [ 5, -2, 9 ]는 이전 단계에 그대로 9을 더한 것이다. 그러므로 두 가지 경우로 나뉜다.
1) [ 9 ]
2) [ -2, 9 ] 와 [ 5, -2, 9 ]
2)는 쉽게 최대합을 구할 수 있다. 이전 단계 최대 Sum은 3이었다. 고로, 3 + 9를 하면 12이다.
1) 9
2) 12
1)과 2)를 비교하면 최대 Sum은 12가 된다. 이를 공식으로 나타내면 아래와 같다.
포인터가 인덱스 n을 가리킬 때, 최대합을 F(n)이라고 해보자.
1) I(n) ( = 현재값 )
2) F(n-1) + I(n)
1)과 2) 중 큰 값이 F(n)이 된다. 이제 이를 배열로 만들어서 풀어보자.
1) [ 5 ]
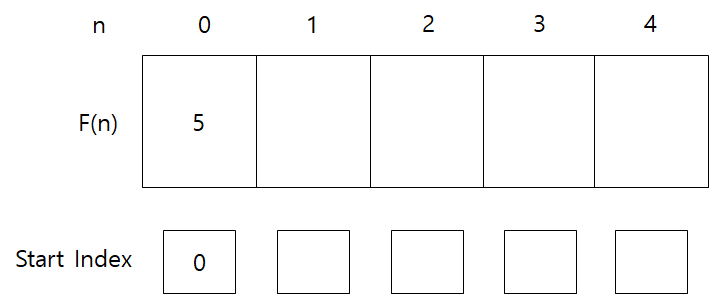
1) I(n) = 5
2) F(n-1) + I(n) = 0 + 5
→F(0) = 5
2) [ 5 , -2 ]

1) I(n) = -2
2) F(n-1) + I(n) = 5 + -2
→F(1) = 3
인덱스 0부터 합해져 온 2)가 더 크므로 Start Index는 0이다.
3) [ 5, -2, 9 ]

1) I(n) = 9
2) F(n-1) + I(n) = 3 + 9
→F(2) = 12
인덱스 0부터 합해져 온 2)가 더 크므로 Start Index는 0이다.
4) [ 5, -2, 9 , -15 ]
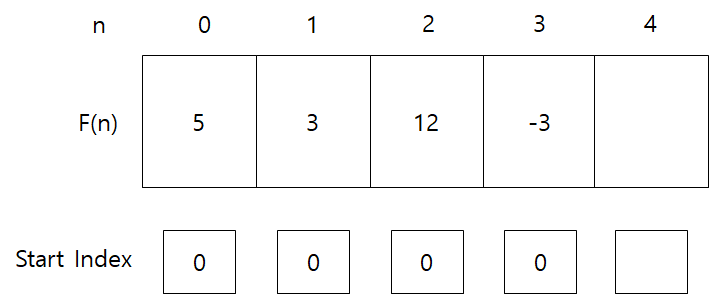
1) I(n) = -15
2) F(n-1) + I(n) = 12 + -15
→F(3) = -3
인덱스 0부터 합해져 온 2)가 더 크므로 Start Index는 0이다.
4) [ 5, -2, 9 , -15, 8 ]
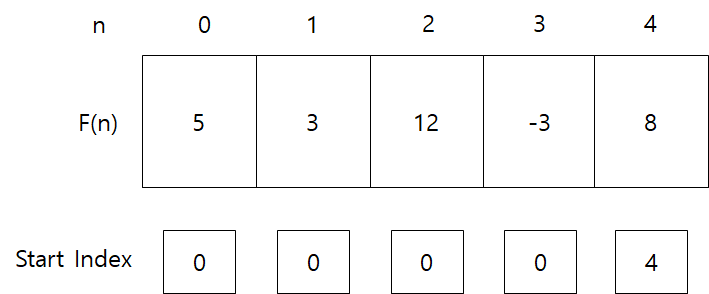
1) I(n) = 8
2) F(n-1) + I(n) = -3 + 8
→F(3) = 8
1)이 더 크므로 Start Index는 자신(4)이 된다.
F(n) 배열의 값중 가장 큰 값은 12이다. F(2)는 StartIndex가 0이므로 0부터 2까지의 부분수열의 합이다. 고로 최대합을 만드는 부분수열은 [ 5 , -2 , 9 ] 가 된다.
참고자료
'문제풀이 > 알고리즘' 카테고리의 다른 글
| [동적계획법] Longest Palindrome SubString (0) | 2021.11.07 |
|---|---|
| [동적계획법] Maximum Product SubArray (0) | 2021.11.07 |
| [동적계획법] Decoding Ways (0) | 2021.11.05 |
| [동적계획법] 최소 동전 개수 ( Min Coin Change ) (0) | 2021.11.05 |
| [동적계획법] 최소 경로 비용 합 ( Minimum Path Sum ) (0) | 2021.11.05 |
