퍼셉트론은 선형적으로
구분 가능한 경우 유용하지만
그렇지 못하면
성능을 발휘하지 못한다.
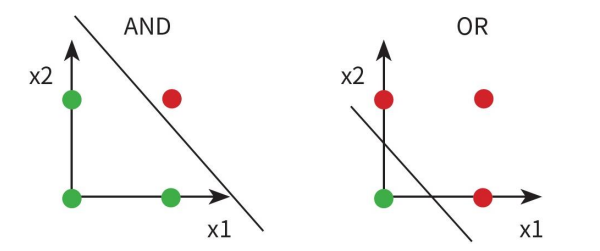
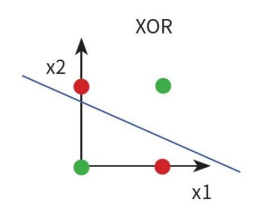
이런 한계를 극복하고자 MLP(Multilayer Perceptron)가 등장했다.
MLP ( Multilayer Perceptron )
핵심 아이디어
1) 은닉층을 둔다.
2) 시그모이드(Sigmoid) 활성함수를 도입한다.
3) 오류 역전파(Back Propagation) 알고리즘을 사용한다.
1. 다층 퍼셉트론 ( 은닉층 )
인공지능의 목적은 '특징'을 토대로 결과를 '예측' 및 '분류'하는 것이다.
기계학습은 '특징 추출'을 인간이 담당한다. 인간의 주관이 담긴 특징을 토대로 학습이 이루어지기에 인간의 사고 범위 내에서 학습이 이루어진다.
인공신경망은 특징추출을 직접한다. 스스로 이미지나 영상의 특징을 추출하여 가중치를 부여하고 이를 토대로 '판단'을 한다. 은닉층은 인공지능이 자발적으로 특징을 추출하는 층이다.
인공신경망의 기본단위는 퍼셉트론이다.
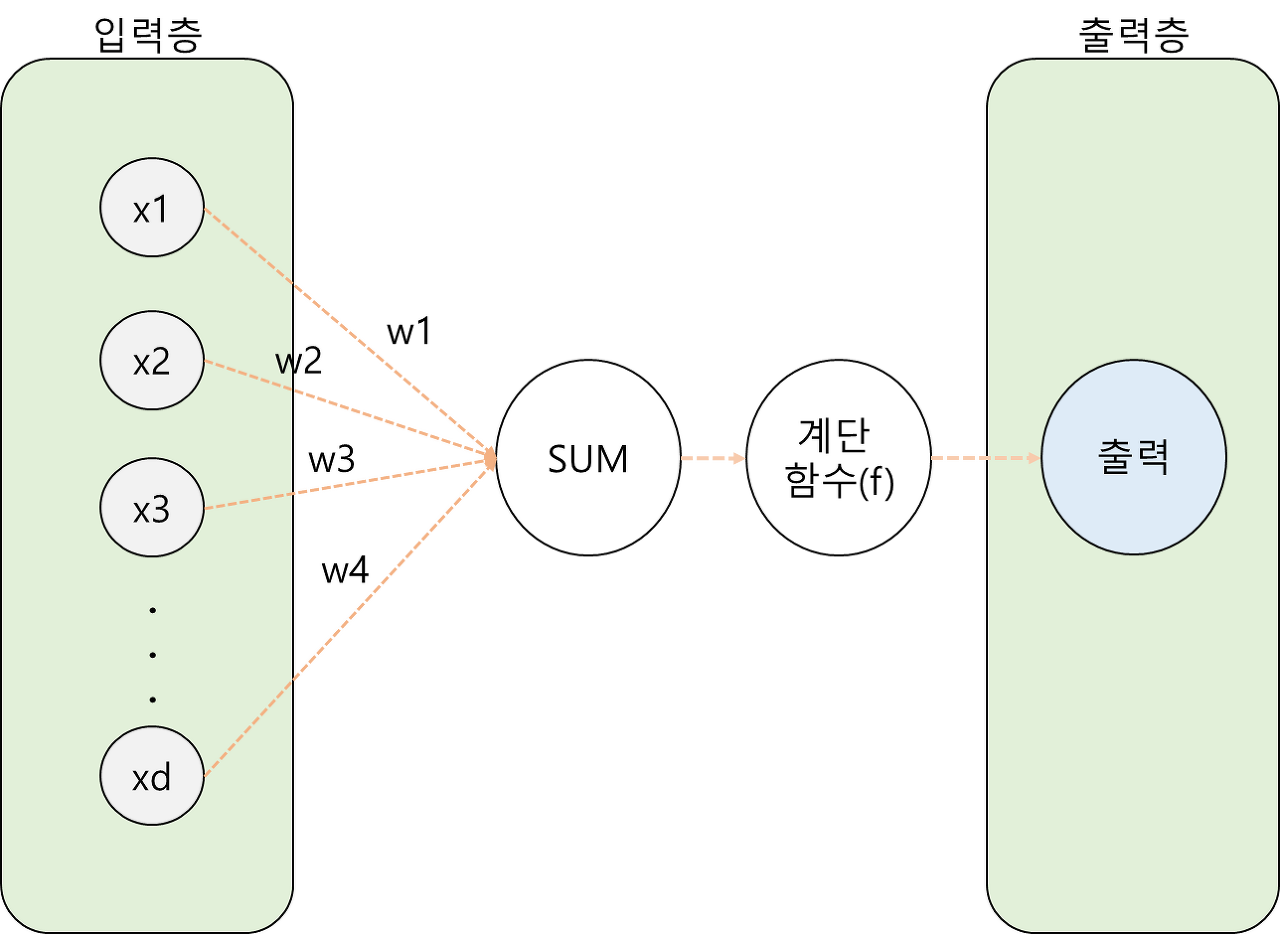
단순한 퍼셉트론은 입력층과 출력층 밖에 없다.
입력이 들어오면 연산하여 바로 판단한다.
어떤 그림의 색상이 무엇이냐? 점이냐 선이냐?와 같은 저차원 영역의 판단은 가능하지만 이미지가 호랑이이냐? 곰이냐? 같은 고차원 영역의 판단은 입력된 데이터를 가공하는 과정이 필요하다.
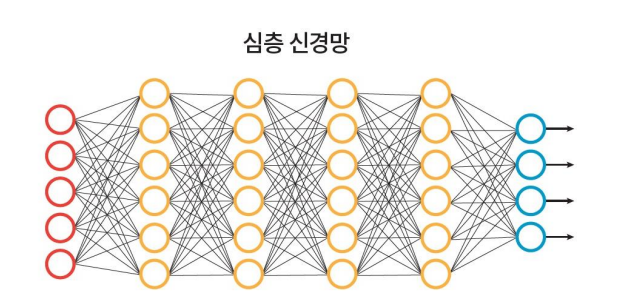
빨간 원은 입력층, 노란 원은 은닉층, 파란 원은 출력층이다. 신경망을 이해하기 위해 툴을 하나 이용해보자.
Tensorflow — Neural Network Playground
Tinker with a real neural network right here in your browser.
playground.tensorflow.org
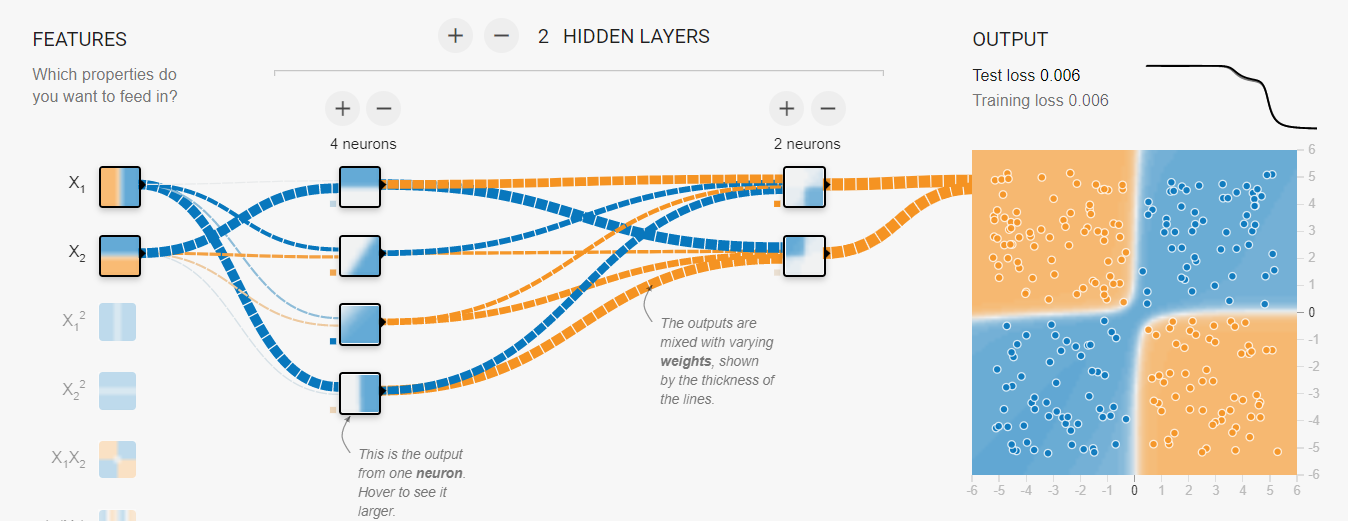
위 사이트는 뉴럴 네트워크를 구현하고 테스트할 수 있는 사이트이다.
단순 퍼셉트론이 해결하지 못하는 XOR 데이터를 은닉층 두 개를 두고 sigmoid 함수를 이용하여 데이터를 분류(Classfication)하는 과정을 시연해보면 아래와 같다.
1) 입력층
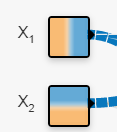
초기 입력 데이터는 단순하다. 그저 가로, 세로로 구역을 나눈 데이터이다.
초기 입력 데이터에 가중치를 어떻게 부여하느냐에 따라 데이터는 한 차원 높아진다.
2) 첫 번째 은닉층
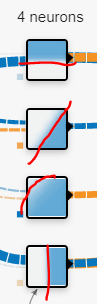
단순한 가로 세로를 넘어서 한 층 복잡해진 영역 구분이 만들어졌다.
복잡해진 데이터에 가중치를 부여하여 한 차원 높은 데이터를 만들어 보자.
2) 두 번째 은닉층
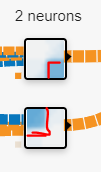
영역 구분이 한 차원 더 정밀해지고 세밀해졌다.
3) 출력층
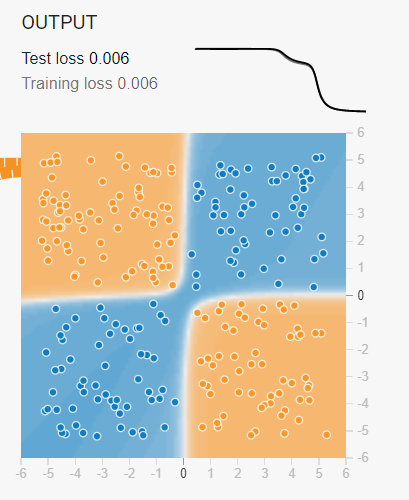
차원이 높아진 분류 모델이 만들어지면서 손실율도 0.006까지 떨어졌다. 단순 선형으로만 분류 가능했던 퍼셉트론은 은닉층을 둠으로써 고차원의 분류가 가능해진다.
2. 시그모이드 활성함수
데이터들은 가중치가 부여된 후 모두 합해진다.
SUM = x1*w1 + x2*w2
그리고 합(SUM)은 활성함수(f)의 변수로 사용된다. 활성함수는 분류기(Classfier)로 사용된다. 지난 포스팅에서 다룬 계단함수는 아래와 같다.
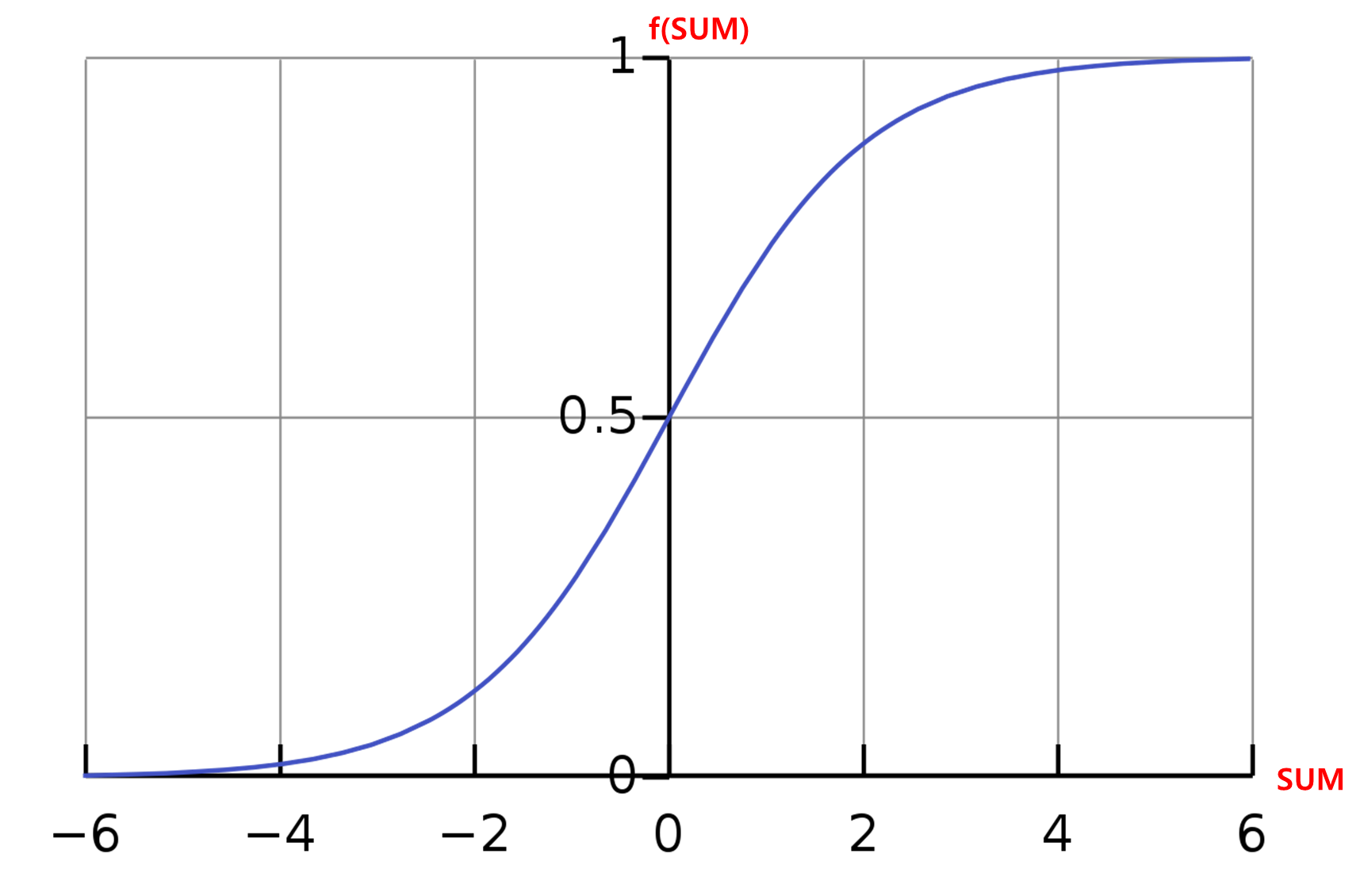
f(SUM)이 특정값(Θ)보다 크면 1 작으면 -1이었다. 명제논리처럼 참이냐 거짓이냐와 같은 이산적 논리로 데이터를 판단하는 것이 계단함수이다.
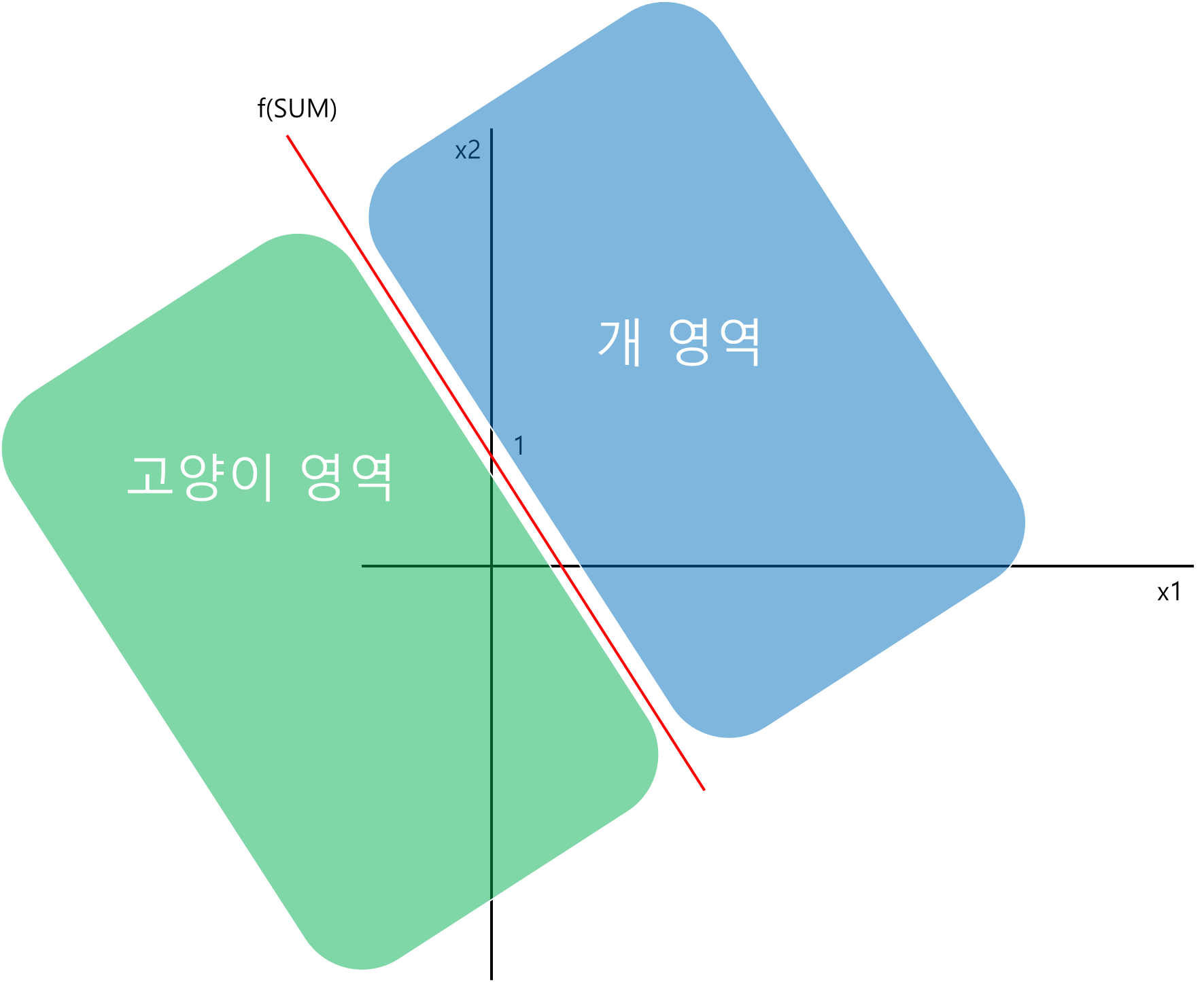
하지만 세상은 참과 거짓으로 나뉘지 않는다. 세상은 좀 더 불확실하다. 그래서 1 과 -1 보다는 1 과 0 사이의 확률, 즉 신뢰도로 나타내는 것이 조금 더 정확하다. 이때 사용되는 함수가 시그모이드 함수이다.
SUM이 개나 고양이일 확률, 즉 신뢰도( f(SUM) )를 구한다. SUM 데이터가 신뢰도가 낮게 측정된다면 '손실'이 크다고 판단한다. 이때 손실정도를 나타내는 함수가 '손실함수'이다.
3. 손실함수
학습이란 손실을 최소한으로 줄이는 것이다. 손실을 줄이려면 '가중치'를 조절해야한다. 가중치를 조절하기 위해 '미분'이 사용된다.
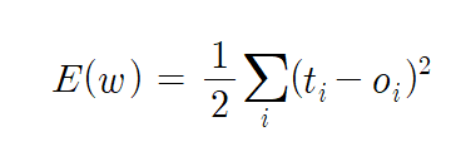
ti는 1이나 0 같은 정답이다. oi는 시그모이드 함수로 도출된 신뢰도이다. 정답과 도출된 신뢰도의 차이의 제곱이 손실함수이다.
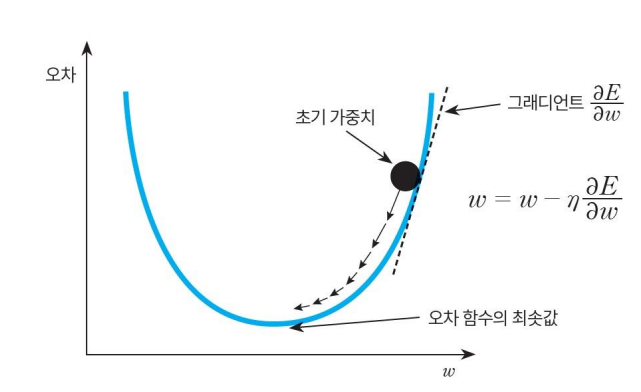
가중치(w)에 따른 오차(손실) 그래프이다. 손실에 따른 오차가 최소가 되는 지점을 구하려면
기울기가 양수인 지점에서는 좌측으로
기울기가 음수인 지점에서는 우측으로 이동해야한다.
현재 w에 기울기를 빼주면 가중치가 조절된다.
w에 양수인 기울기를 빼면 좌측으로 이동하고 w에 음수인 기울기를 빼면 우측으로 이동한다.
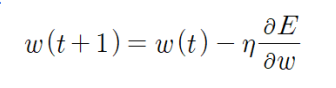
현재의 가중치를 w(t)라 할 때, 다음 가중치는 w로 손실함수(E)의 도함수를 구하여 빼준 뒤 임의로 정한 학습률을 곱해주어 다음 가중치(w(t+1))를 결정한다. 그리고 조절된 가중치로 분류 모델의 손실율을 따져본다.
이처럼 가중치(w)를 조절하여 분류모델의 손실율을 최소한으로 줄이는 모델을 만들어가는 과정이 '학습(Learning)'이다.
'CS > 인공지능' 카테고리의 다른 글
| [인공지능] 퍼셉트론(Perceptron) (0) | 2021.12.14 |
|---|---|
| [인공지능] 기계학습 ( 클러스터링 ) (0) | 2021.12.13 |
| [인공지능] 기계학습 ( 분류기; Classifier ) (0) | 2021.12.13 |
| [인공지능] 기계학습 ( 경사하강알고리즘 ) (0) | 2021.12.13 |
| [인공지능] 기계학습 (선형회귀) (0) | 2021.12.12 |
