다익스트라 알고리즘(Dijkstra)
다익스트라 알고리즘은 특정지점에서 다른지점으로 가는 최단경로를 구하는 알고리즘이다. 다익스트라 알고리즘은 그리디(Greedy) 알고리즘 기반으로 한다. 그리디(Greedy) 알고리즘은 '현재'를 기준으로 최적해를 구하는 알고리즘이다.
네비게이션을 떠올리면 이해가 쉽다.
네비게이션은 차가 위치한 '현재'를 기점으로 최단경로를 탐색한다.

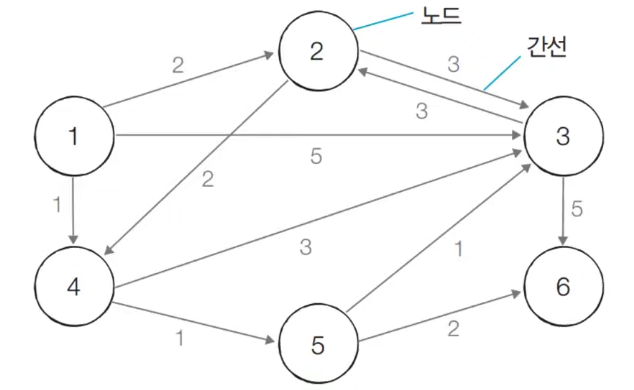
A와 B는 5L의 기름으로 연결된다. A와 B는 '노드'이고 5L의 기름은 '간선'이다.
그럼 차가 A에서 출발하여 E로 간다고 가정해보자.
네비게이션이 A -> B -> D -> E 경로가 최적이라 알려주어도 운전자가 C로 이동하면 네비게이션은 C에서의 최단경로를 파악해야 한다. '현재'를 기준으로 최적해를 구해야 한다는 의미다. 또한 A -> B -> C -> A 로 가면 안 된다. 기름은 양수이다. 과거에 들린 지점을 다시 들리면 기름만 더 든다. 최적이라 할 수 없다. A에서 B로 이동하면 5L의 기름이 소비되지 기름이 채워지는 마법은 일어나지 않는다.
그러나 마법이 아닌 요런 이벤트가 있을 수 있다.

B - C 경로에 기름무료나눔 이벤트가 열렸다
B - C 경로는 3L의 기름이 소비되지만 무료로 20L를 나누어주니 총 17L 이득이다.
최단경로의 의미가 오로지 기름을 최소로 사용함을 기준으로 한다면 A에서 B로 가는 최단경로는 A->B가 아니다.
A -> B -> C -> A -> B -> C -> A ....
순환을 하면 할수록 4L( 5L + 8L - 17L )의 기름을 추가로 얻을 수 있다. 개이득이다. 이렇게 되면 다익스트라 알고리즘으로 최단경로를 구하는 의미가 사라진다. 다익스트라 알고리즘은 이런 이벤트적 요소를 케어하지 못한다. 음의 간선이 있는 경우는 벨만포드 알고리즘을 사용한다. 해당 알고리즘은 차차 알아보겠다.
다익스트라 알고리즘(Dijkstra)은 양의 간선인 그래프(Graph)에서 현재를 기준으로 최단경로를 파악하는 알고리즘이다.
알고리즘 원리
Greedy 기반이므로 현재를 기준으로 최단경로를 갱신하는 방식으로 알고리즘은 진행된다.

최단경로 자료구조
| A | B | C | D | E |
| 0 | ∞ | ∞ | ∞ | ∞ |
최단경로를 저장한 자료구조를 갱신할 것이다. 출발지 A는 0이고 나머지 노드는 무한이 디폴트이다.
➢ 현재 노드 : A
1) 인접노드의 최단경로 구하기
A는 B와 C로 갈 수 있다.
B : 5L(A->B) + 0(A->A 최단경로) = 5L
C : 8L(A->C) + 0(A->A 최단경로) = 8L
2) 최단경로 자료구조 갱신
B : 5L < 무한 이므로 5L로 갱신
C : 8L < 무한 이므로 8L로 갱신
| A(탐색완료) | B | C | D | E |
| 0 | 5L | 8L | ∞ | ∞ |
3) 최단경로 자료구조에서 탐색되지 않고 값이 최소인 노드를 현재노드로 지정
➢ 현재 노드 : B
1) 인접노드의 최단경로 구하기
B는 C와 D로 갈 수 있다.
D : 1L(B->D) + 5L(A->B의 최단경로) = 6L
C : 3L(B->C) + 5L(A->B의 최단경로) = 8L
2) 최단경로 자료구조 갱신
D : 6L < 무한 이므로 6L로 갱신
C : 8L = 8L 같으므로 유지
| A(탐색완료) | B(탐색완료) | C | D | E |
| 0 | 5L | 8L | 6L | ∞ |
3) 최단경로 자료구조에서 탐색되지 않고 값이 최소인 노드를 현재노드로 지정
➢ 현재 노드 : D
모든 노드를 탐색할 때까지 위 과정을 반복한다. 다익스트라 알고리즘은 이처럼 현재 노드를 기준으로 최단경로 자료구조를 갱신하는 방법으로 나아간다. 이를 코드로 구현해보자.
코드 구현( Python )
가장 단순한 방법으로 코드를 구현해보겠다. 노드가 V개라면 시간복잡도가 O(V²)인 방식이다.
import sys
input = sys.stdin.readline # 데이터 수가 많은 경우, 더 빠르게 동작하도록 도와주는 함수
INF = int(1e9) #무한
n,m = map(int,input().split()) # n = 노드의 수, m = 간선의 수
start = int(input()) # 시작 지점
graph = [ [] for i in range(n+1) ] # 그래프 자료구조
visited = [False]*(n+1) # 탐색이력 자료구조
distance = [INF]*(n+1) # 최단경로 자료구조
#그래프 자료구조 초기화
for _ in range(m) :
node,target,value = map(int,input().split()) # target : 인접노드, value : 간선비용
graph[node].append((target,value)) # 노드에 (인접노드,간선비용) 추가
#탐색이력 없고 최단경로가 최솟값이 노드 반환
def get_smallest_node() :
minValue = INF
minIndex = 0
for i in range(1, n+1) : #탐색이력 없는 최단경로를 가진 노드 탐색
if not visited[i] and distance[i] < minValue :
minValue = distance[i]
minIndex = i
return minIndex
#다익스트라 알고리즘
def djikstra(start) :
#START 초기화
visited[start] = True #탐색이력 TRUE
distance[start] = 0 #출발지 최단거리 : 0
for line in graph[start] : # 인접노드 정보 가져오기
distance[line[0]] = line[1] # 최단경로 자료구조 초기화
# 알고리즘 시작
for i in range(n) :
index = get_smallest_node() # 탐색이력 없고 최단경로가 최솟값인 노드 생성
visited[index] = True # 탐색이력 TRUE
for line in graph[index] : # 인접노드 정보 가져오기
cost = distance[index] + line[1] # 비용계산
if cost < distance[line[0]] :distance[line[0]] = cost # 최단경로 갱신
#Greedy 반복
djikstra(start) #다익스트라 알고리즘 실행
# 출력
for i in range(1,n+1) :
if distance[i] == INF : print("INFINITY")
else : print(distance[i])
다음 포스팅에서는 개선된 다익스트라 알고리즘을 다루어보겠다.
참고자료
이것이 취업을 위한 코딩 테스트다 with 파이썬 - YES24
나동빈 저자의 유튜브 라이브 방송 https://www.youtube.com/c/dongbinnaIT 취준생이라면 누구나 입사하고 싶은 카카오 · 삼성전자 · 네이버 · 라인!취업의 성공 열쇠는 알고리즘 인터뷰에 있다!IT 취준생
www.yes24.com
'문제풀이 > 알고리즘' 카테고리의 다른 글
| [Algorithm] 플로이드-워셜(Floyd-Warshall) 알고리즘이란? (0) | 2023.05.17 |
|---|---|
| [Algorithm] 개선된 다익스트라 알고리즘 (0) | 2023.05.15 |
| [알고리즘] BFS(Breadth-First Search) 탐색 알고리즘이란? (0) | 2023.03.28 |
| [알고리즘] DFS(Depth-First Search) 탐색 알고리즘이란? (0) | 2023.03.28 |
| [알고리즘] 분할정복(Divide&Conquer) 이란? (0) | 2023.02.14 |
