[Algorithm] 다익스트라 알고리즘(Dijkstra)이란?
다익스트라 알고리즘(Dijkstra) 다익스트라 알고리즘은 특정지점에서 다른지점으로 가는 최단경로를 구하는 알고리즘이다. 다익스트라 알고리즘은 그리디(Greedy) 알고리즘 기반으로 한다. 그리디(
lordofkangs.tistory.com
이전 포스팅에서 최단경로 알고리즘으로 다익스트라 알고리즘을 알아보았다.
다익스트라 알고리즘은 시작점이 고정되어 있을때 모든노드로 가는 최단경로를 테이블로 관리하였다. 플로이드-워셜 알고리즘은 시작점이 모든 노드인 경우, 다른 모든 노드로 가는 최단경로를 테이블로 관리하는 알고리즘이다.
1. 자료구조 : 2차원 테이블
다익스트라 알고리즘의 최단경로 테이블은 1차원 테이블로 구성 가능했다.
| A->A(시작점) | A->B | A->C | A->D |
| 3 | 7 | 12 | 15 |
플로이드-워셜 알고리즘은 시작점이 1개에서 n개로 증가한만큼 1차원 테이블도 n개 증가한 2차원테이블이 필요하다.

2. 알고리즘

출발과 도착에는 두 가지 노선이 있다.
◉ 직행노선
◉ 경유노선
1) 직행노선으로 최단경로 테이블 갱신하기
그래프의 간선은 인접노드의 직행노선을 가리킨다. 그러므로 먼저 직행노선으로 테이블을 갱신한다.

직행노선이 없는 경우, 무한으로 표시한다.
2) 경유노선으로 최단경로 테이블 갱신하기
직행보다 오히려 경유노선이 최단경로일 수 있다. 경유노선이 가능한 모든 경우를 탐색하여 최단경로 테이블을 갱신해야 한다.
경유노선 완전탐색을 해보자.
1) A를 경유하는 경우 ( 6가지, ₃P₂ )
B ▹ A ▹ C
B ▹ A ▹ D
C ▹ A ▹ B
C ▹ A ▹ D
D ▹ A ▹ B
D ▹ A ▹ C
B ▹ A 는 직행경로만을 의미하지 않는다. 최단경로 테이블에는 다양한 경로의 값이 누적된다. 예를 들어, B ▹ A 값은 B ▹ C ▹ A 일수도 B ▹ A 일수도 있다. A를 경유하는 D ▹ C 최단거리를 구한다면 아래와 같이 표현할 수 있다.
※ D ▹ C 최단거리 = min ( D ▹ C 최단거리테이블 값, ( D ▹ A 최단거리테이블 값 + A ▹ C 최단거리테이블 값 ) )
두 값 중 최솟값을 최단거리 테이블로 갱신한다.
경유점, 시작점, 도착점
이렇게 3가지 요소에 따라 경우의 수가 생성되므로 완전탐색을 구현하려면 3중for문을 구현해야한다.
이런 원리로 A,B,C,D 모든 경우를 완전탐색하면 최신테이블의 데이터를 갱신하면 최종 최단거리 테이블이 완성된다.
코드구현 (Python)
INF = int(1e9) #무한
n = int(input()) #노드의 수
m = int(input()) #간선의 수
#2차원 테이블 만들기
graph = [[INF]*(n+1) for _ in range(n+1)]
#출발점과 도착점이 동일한 경우 0으로 초기화
for x in range(1,n+1) :
for y in range(1,n+1) :
if x == y :
graph[x][y] = 0
#간선정보 초기화하기
for _ in range(m) :
start,end,value = map(int,input().split())
graph[start][end] = value
#플로이드-워셜 알고리즘 구현 ( 3중 for문 )
for middle in range(1,n+1) : # 경유점
for start in range(1,n+1) : # 시작점
for end in range(1,n+1) : # 도착점
current = graph[start][end] # 현재 최단경로
value = graph[start][middle] + graph[middle][end] # 경유시 최단경로
graph[start][end] = min(current,value) # 최단경로 초기화
#출력
for start in range(1,n+1) :
for end in range(1,n+1) :
if graph[start][end] == INF : print("INFINITY")
else : print(graph[start][end],end=" ")
print()
코드구현 (JAVA)
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
import static java.lang.Math.*;
//BOJ11404 플로이드
public class Main {
static int n,m;
static final int INF = Integer.MAX_VALUE;
static int[][] floyd;
public static void main(String[] args) throws IOException {
init();
solution();
print();
}
private static void solution() {
for(int mid=1;mid<=n;mid++){
for(int start=1;start<=n;start++){
for(int end=1;end<=n;end++){
if(floyd[start][mid] == INF || floyd[mid][end] == INF) continue;
int cost = floyd[start][mid] + floyd[mid][end];
floyd[start][end] = min(floyd[start][end],cost);
}
}
}
}
private static void init() throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
n = Integer.parseInt(br.readLine());
m = Integer.parseInt(br.readLine());
floyd = new int[n+1][n+1];
for(int i=0;i<n+1;i++){
for(int j=0;j<n+1;j++){
if(i==j) floyd[i][j] = 0;
else floyd[i][j] = INF;
}
}
for(int i=0;i<m;i++){
StringTokenizer st = new StringTokenizer(br.readLine());
int start = Integer.parseInt(st.nextToken());
int des = Integer.parseInt(st.nextToken());
int cost = Integer.parseInt(st.nextToken());
floyd[start][des] = min(floyd[start][des],cost);
}
}
private static void print() {
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
if(floyd[i][j] != INF) System.out.print(floyd[i][j]+" ");
else System.out.print(0 + " ");
}
System.out.println();
}
}
}
▹ 입력
4
7
1 2 4
1 4 6
2 1 3
2 3 7
3 1 5
3 4 4
4 3 2
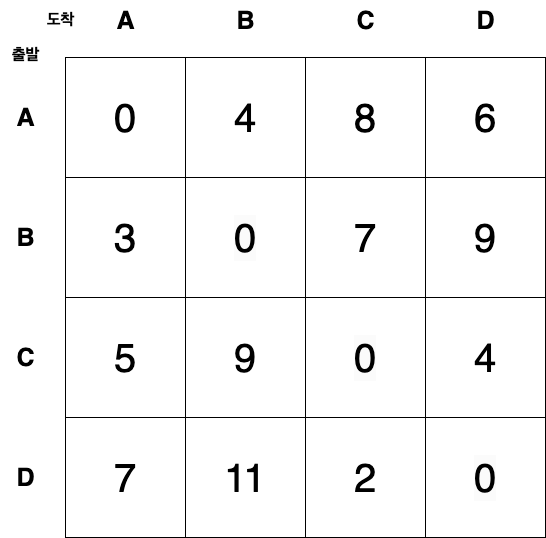
▹ 결과
0 4 8 6
3 0 7 9
5 9 0 4
7 11 2 0
참고자료
이것이 취업을 위한 코딩 테스트다 with 파이썬 : 네이버 도서
네이버 도서 상세정보를 제공합니다.
search.shopping.naver.com
'문제풀이 > 알고리즘' 카테고리의 다른 글
| [Algorithm] 무방향그래프에서 싸이클 찾기 (0) | 2023.05.23 |
|---|---|
| [Algorithm] Union-Find 알고리즘이란? ( with 서로소 집합 자료구조 ) (0) | 2023.05.22 |
| [Algorithm] 개선된 다익스트라 알고리즘 (0) | 2023.05.15 |
| [Algorithm] 다익스트라 알고리즘(Dijkstra)이란? (1) | 2023.05.13 |
| [알고리즘] BFS(Breadth-First Search) 탐색 알고리즘이란? (0) | 2023.03.28 |
