반응형
위상정렬은 방향그래프를 한 정렬이다.
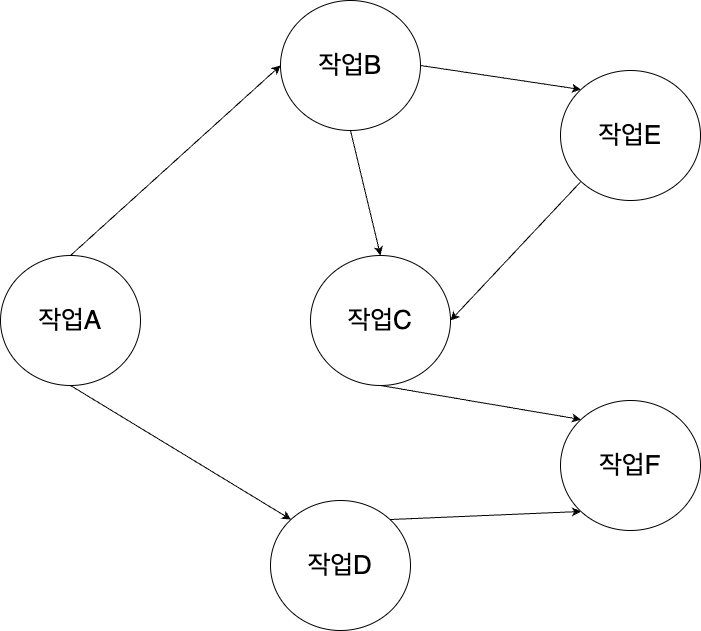
위 그래프는 작업 간 의존관계를 표현한다. 작업C는 작업B와 작업E가 완료되어야 처리가 가능하다. 그래프는 의존관계는 표현하지만 어떤 작업부터 처리해야 하는지 알려주지는 않는다.
위상정렬(Topology Sort)
◎ 알고리즘
위상 정렬의 조건은 하나이다.
☑︎ 전처리 작업이 완료된 순서대로 작업이 진행되어야 한다.
이를 어떻게 구현할까?
방향그래프는 방향을 가진 간선을 가지고 있다. 노드로 들어오는 간선의 개수를 진입차수라고 한다. 작업C는 진입차수가 2이다.
간선① : 작업B ➠ 작업C
간선② : 작업E ➠ 작업C
작업B가 완료되면 작업B는 간선①을 제거한다.
작업E가 완료되면 작업E는 간선②를 제거한다.
작업C는 진입차수가 0이된다. 그럼 큐에 들어가서 선입선출을 대기한다.
큐에서 POP되는 순서가 작업순서가 된다.
◎ 자료구조
- 진입차수 테이블 : 각 노드의 진입차수 데이터를 저장한다. 진입차수가 0인 노드만 큐에 등록된다.
- 그래프 : 간선정보를 저장한다. 각 노드의 의존관계를 나타낸다.
◎ 코드
from collections import deque
n,e = map(int,input().split())
#자료구조
indegree = [0]*(n+1) #진입차수테이블
graph = [[] for i in range(n+1)] #그래프테이블 (노드 간 의존관계)
#그래프 간선 초기화
for _ in range(e) :
a,b = map(int,input().split())
graph[a].append(b)
indegree[b] += 1
#위상정렬 알고리즘
def topology_sort() :
q = deque() #큐생성
result = [] #결과테이블
#진입차수가 0인 노드 탐색
for i in range(1,n+1) :
if indegree[i] == 0 : q.append(i) #큐에 등록
while q : #큐가 비어질때까지 반복
now = q.popleft() #선입선출
result.append(now)
# 의존관계 노드 가져오기
for node in graph[now] :
indegree[node] -= 1 #진입차수 제거
#진입차수가 0이면 큐에 등록
if indegree[node] == 0 :
q.append(node)
#출력
for value in result :
print(value,end=" ")
topology_sort()
- 입력
7 8
1 2
1 5
2 3
2 6
3 4
4 7
5 6
6 4
- 결과
1 2 5 3 6 4 7
참고자료
이것이 취업을 위한 코딩 테스트다 with 파이썬 : 네이버 도서
네이버 도서 상세정보를 제공합니다.
search.shopping.naver.com
반응형
'문제풀이 > 알고리즘' 카테고리의 다른 글
| [Algorithm] 이분그래프(Bipartite Graph) ( + BOJ1707 ) (0) | 2023.06.23 |
|---|---|
| [Alogorithm] 세그먼트 트리 ( Segment Tree ) (0) | 2023.06.21 |
| [Algorithm] 크루스칼 알고리즘(Kruskal Algorithm)이란? (0) | 2023.05.24 |
| [Algorithm] 무방향그래프에서 싸이클 찾기 (0) | 2023.05.23 |
| [Algorithm] Union-Find 알고리즘이란? ( with 서로소 집합 자료구조 ) (0) | 2023.05.22 |
