우리는 좀 더 빠른 성능의 탐색을 위해
이진탐색트리를 사용한다.
배열은 탐색시,
n개의 데이터를 최대 n번 비교한다.
하지만 이진탐색트리는 다르다.

탐색하려는 값과 기준이 되는 노드를 비교하여, 크면 오른쪽으로 작으면 왼쪽으로 가서 매 비교때 마다 탐색할 노드의 수가 반씩 줄어든다.
데이터의 수가 8개가 있다면 배열은 최악의 경우, 8번의 탐색을 해야하지만, 하지만 이진트리는 log 8 즉, 단 3번 만에 원하는 데이터를 찾을 수 있다. 그러므로 이진탐색트리에서 높이(h)의 개념은 중요하다.
트리의 높이는 곧 탐색 횟수를 의미한다. 그러므로 높이(h) = log n 이다. 그러나 이는 균형잡힌 이진트리에서만 적용되는 개념이다.
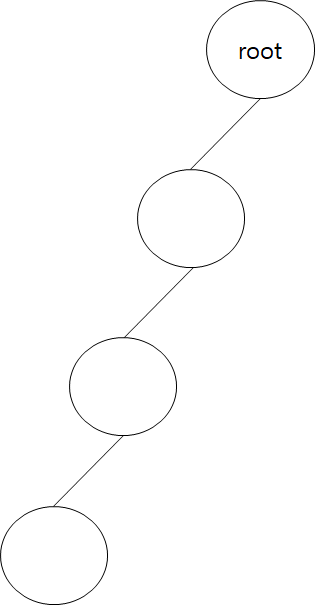
만약 이진탐색트리가 이렇게 되어 있다면, 배열처럼 n개의 데이터를 최대 n번 만에 탐색할 것이다. 그래서 이진탐색트리를 균형잡힌 트리로 만들면 탐색할 데이터로 어떤 값이 들어와도 log n의 성능을 낼 수 있다.
레드-블랙 트리 (Red-Black Tree)
레드-블랙 트리는 균형이진탐색 트리 중 가장 유명하고 많이 사용되는 트리이다. 레드 블랙 트리가 되려면 다섯 가지 조건을 충족해야한다.
1. 모든 노드는 블랙 아니면 레드여야 한다.
2. 루트는 블랙 노드이다.
3. 잎 노드는 블랙이어야 한다.
4. 레드 노드의 자식은 블랙이어야 한다.
5. 각 노드에서 잎 노드까지의 경로 안에 블랙 노드의 수는 모두 동일해야한다.
이진탐색 트리가 한 쪽으로 쏠리지 않고 균형을 유지하려면 이와 같은 조건을 충족해야한다.
O(log n) 증명
Part 1.
증명을 위해서는 한 가지 사실을 먼저 증명해야한다.
V : 해당 노드
h(V) : 노드의 높이
bh(V) : 해당 노드에서 잎노드까지 블랙노드의 개수 (V 제외)
V의 서브트리의 내부노드 개수 >= 2bh(V)-1
위 부등식이 항상 참임을 먼저 증명해야한다.
레드블랙 트리는 잎노드가 모두 null노드이다. 그리고 잎 노드는 조건에 따라 블랙노드이다. 그리고 잎노드가 아닌 모든 노드를 내부노드라고 부른다.
그럼 이제 용어정리가 끝났으니,
귀납법으로 위 부등식을 증명해보자.
- h(V) = 0 인 경우
높이가 0이면 잎노드를 의미한다. 잎 노드는 내부노드가 없으니 내부노드의 개수는 0이다. bh(V)는 본인을 제외한 블랙노드의 개수이니 블랙인 잎노드를 제외하면 더 이상 노드가 없으니 bh(V)도 0이다.
그러므로 0 >= 20 -1 = 0 이다.
- h(V) = k 가 성립한다고 가정할 때, h(V) = k+1인 경우
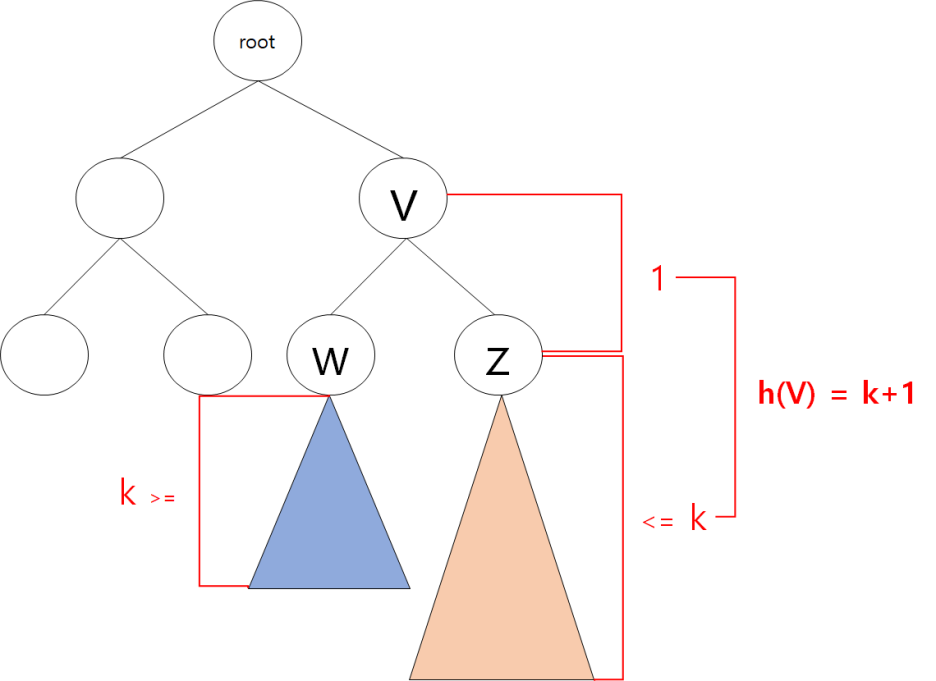
V 노드에서 자식노드까지 높이가 1이고 자식노드의 트리의 높이가 k 이거나 더 작다. V 노드의 서브트리의 노드 개수를 자식 노드를 통해 나타내보자.
V의 서브트리 노드의 개수 >= W의 서브트리 노드의 개수 + Z의 서브트리 노드의 개수 + V의 노드
V의 서브트리 노드의 개수 >= 2bh(W) -1 + 2bh(Z) -1 + 1
W노드의 트리와 Z노드의 트리의 블랙노드의 개수는 V노드 트리의 블랙노드 개수에서 W, Z노드를 제외한 개수이다.
bh(W), bh(Z) >= bh(V) -1
이제 위의 식에 해당 부등식을 대입해보자.
V의 서브트리 노드의 개수 >= 2bh(V)-1 -1 + 2bh(V)-1 -1 + 1
V의 서브트리 노드의 개수 >= 2*2bh(V)-1 -1
V의 서브트리 노드의 개수 >= 2bh(V) -1
그러므로
V의 서브트리의 내부노드 개수 >= 2bh(V)-1
가 증명되었음을 알 수 있다.
Part 2.

root와 잎노드들은 모두 블랙 노드여야 하며, 레드의 자식도 블랙 노드여야한다. 그래서 root부터 잎 노드까지 탐색 횟수가 h이면 그 중 블랙노드의 개수는 >= h/2이다.
bh(Root) >= h/2
Root 노드의 서브트리의 내부노드 개수는 앞서 증명한 공식을 이용하면 이렇게 된다.
Root 노드의 서브트리의 내부 노드 개수 (n) >= 2bh(Root) - 1
그럼 여기서 bh(Root) >= h/2을 대입하면 아래와 같이 된다.
n >= 2h/2 -1
n+1 >= 2h/2
log(n+1) >= h/2
h <= 2 * log(n+1)
레드-블랙 트리의 높이(h) 다시 말하면, 최대 탐색 횟수는 2log(n+1)이다. 이를 빅오 표기법으로 나타내면 O(log n)이 된다. 그러므로 레드- 블랙 트리는 어떤 데이터를 탐색하든 시간복잡도가 O(log n)을 넘지 않는 균형이진탐색트리다.
참고 자료
'문제풀이 > 알고리즘' 카테고리의 다른 글
| [알고리즘] 퀵 정렬 (Quick Sort)이란? (0) | 2021.08.04 |
|---|---|
| [알고리즘] 버블정렬 향상 시키기 (0) | 2021.08.01 |
| [자료구조] HashMap 파헤치기 2 ( keySet(), values(), iterator() ) (0) | 2021.06.25 |
| [자료구조] HashMap 파헤치기 1 (Linked List + Red Black Tree) (6) | 2021.06.25 |
| [자료구조] 컬렉션 프레임워크 - List (0) | 2021.06.25 |
