시간복잡도 O(N2)과 O(NlogN)의 차이는
분할정복을 하느냐 안 하느냐의 차이이다.
N개의 수를 N번 비교하는게 아니라 (버블정렬)
N개의 수를 분할한 수만큼 비교하는 것이다. (퀵정렬)
[알고리즘] 버블정렬 향상 시키기
버블정렬은 가장 쉽고 이해하기 쉬운 정렬이다. 그러나 시간복잡도가 O(n2)이어서 효율이 좋지 않다. 7개의 수를 일차원 배열에 저장하였다. 이제 버블정렬을 사용하여 오름차순으로 바꾸어 보
lordofkangs.tistory.com
[알고리즘] 퀵 정렬 (Quick Sort)
퀵 정렬(Quick Sort)은 이름 그대로 정렬을 빠르게 하는 알고리즘이다. 그러나 버블정렬에 비해 빠를 뿐, 이름만큼 가장 빠른 정렬 알고리즘은 아니다. 퀵 정렬(Quick Sort) 알고리즘이란? 정렬 알고리
lordofkangs.tistory.com
합병 정렬은 분할정복을 한다.
정렬(Merge Sort)의 분할정복
합병 정렬을 사용하는 가장 큰 장점은 모든 경우의 수에서 시간복잡도가 O(NlogN)으로 일정하다는 것이다. 같은 분할정복인 퀵정렬은 최악의 경우 시간복잡도가 O(N2)이다. 이러한 차이는 분할하는 방식에서 비롯된다.
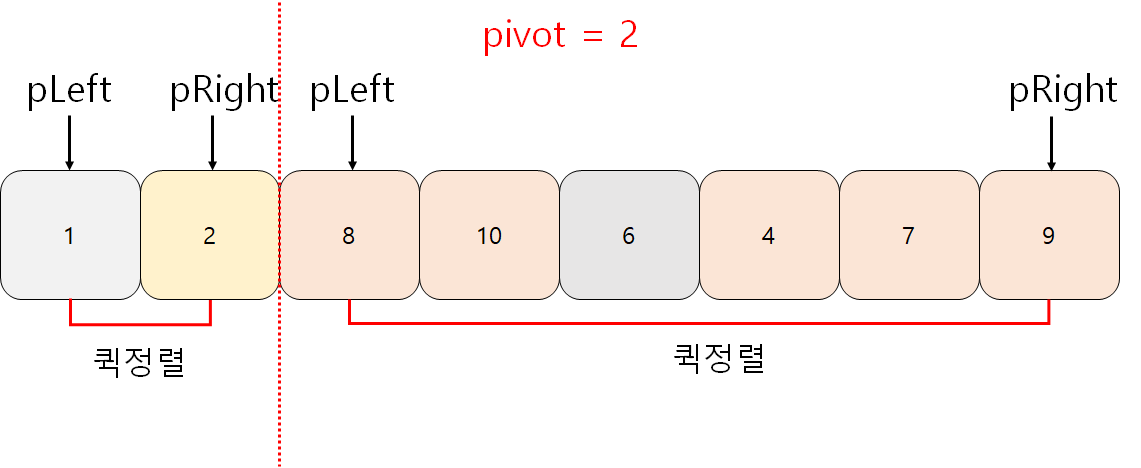
퀵 정렬은 pivot을 기준으로 pivot보다 작은 구간과 큰 구간으로 나뉜다. 그러나 위 그림처럼 pivot보다 작은 수가 별로 없으면 분할이 무색해진다. 그러므로 퀵정렬은 pivot이 중간값에서 많이 벗어나면 성능이 떨어진다.
그러나 합병 정렬은 다르다. 그냥 중간지점에서 두 구간으로 분할한다.

이렇게 pivot 없이 중간에서 배열을 분할하기에 분할 횟수가 일정하다. 그러므로 시간복잡도는 어느 경우의 수에서나 일정하게 유지된다.
그러나 위와 같이 단순하게 중간지점에서 분리하면 한 가지 문제가 발생한다.
퀵정렬은 pivot을 기준으로 좌측과 우측을 나누었다. 그래서 좌측에 있는 수는 이미 우측에 있는 수보다 작은 수이다. (오름차순) 그러나 합병 정렬은 기준없이 중간지점에서 구간을 둘로 나누었다.

그래서 좌측구간이 우측 구간보다 작지 않다. 그러므로 퀵정렬처럼 그냥 합쳐지면 정렬이 되지 않는다. 그러므로 별도의 알고리즘으로 정렬을 완성해야한다.
합병 정렬(Merge Sort) 알고리즘
정렬 알고리즘은 두 가지 원칙에서 비롯된다.
1. 두 수의 대소를 비교한다.
2. 두 수의 위치를 교환한다.
비교와 교환, 이것이 정렬 알고리즘의 근본개념이다.

좌측과 우측은 오름차순 정렬이 완료되었다 가정하자. 정렬을 완성시키려면 '비교'와 '교환'을 해야한다.
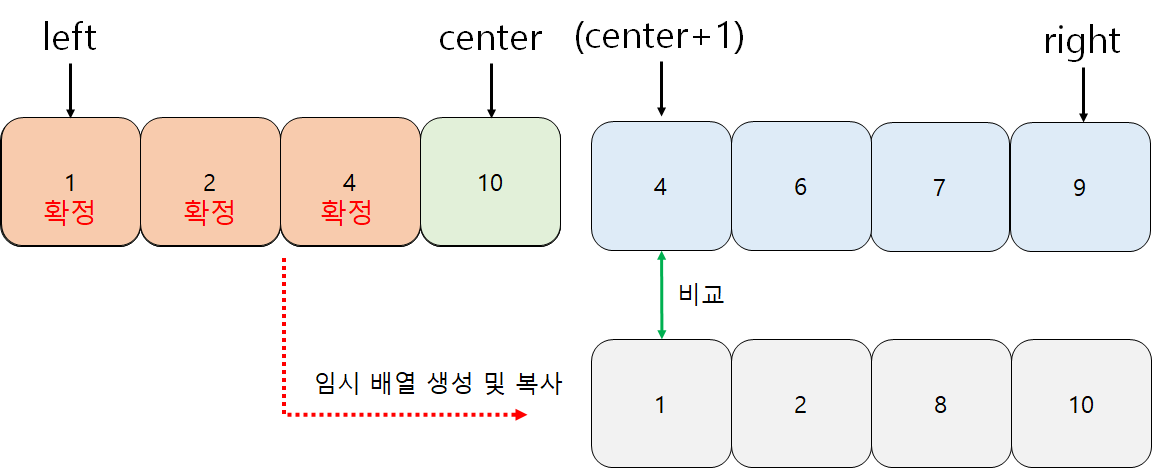
원리는 간단하다. 서바이벌 방식이다. 우선 임시 배열을 하나 생성하여 좌측구간을 복사한다. 그리고 우측구간과 임시배열을 첫 번째 값부터 하나씩 비교한다. 1과 4를 비교하면 1이 작다. 그러므로 배열의 첫 번째 자리는 1의 차지이다.
우측 구간의 4는 그대로 있고 임시배열의 두 번째 값과 비교한다. 2와 4를 비교하면 2가 작다. 배열의 두 번째 자리는 2의 차지이다. 임시 배열의 세 번째 값은 8이다. 8과 4를 비교하면 4가 작다. 배열의 세 번째 자리는 4의 차지이다. 이렇게 좌측구간의 임시배열과 우측구간을 비교하여 배열을 채운다.

우측 구간의 모든 수가 배열에 자리를 차지하였다. 임시배열의 10은 아직 자리가 없다. 그러므로 남은 자리는 10의 차지이다. 이것이 병합 정렬 알고리즘의 비교와 교환 방식이다.
재귀 (recursive)
병합 정렬 알고리즘은 선 분할 후 정렬이다.

먼저 이와 같이 분할을 한 후, 좌측과 우측 구간이 합쳐지면서 병합 정렬 알고리즘이 적용된다. 이렇게 큰 범위에서 작은 범위로 분할되었다가 다시 병합되는 과정에서 알고리즘이 적용되는 방식은 재귀함수로 구현하는 것이 알맞다.
코드
public static void mergeSort(int left, int right) {
if(left < right) {
int center = (left+right)/2;
// 선 분할 ( 재귀 호출 )
mergeSort(left,center);
mergeSort(center+1,right);
// 후 알고리즘 적용
applyMerge(left,right);
}
}
public static void applyMerge(int left, int right) {
int[] buff = new int[right-left+1]; // 임시 배열 생성
int center = (left+right)/2;
int buffSize = 0;
int buffCount = 0;
int arrCount = left;
int i = 0;
// 좌측구간 임시배열 복사
while(arrCount <= center) {
buff[buffSize++] = arr[arrCount++];
}
// 배열 자리 차지하기 서바이벌 시작
for(i=left;i<=right;i++) {
if(buffCount < buffSize && arrCount <= right) {
arr[i] = buff[buffCount] < arr[arrCount] ? buff[buffCount++] : arr[arrCount++];
}else {
break;
}
}
// 우측구간은 남은 자리 그대로 차지하면 된다.
// 그러나 임시배열은 남은 구간에 데이터를 넣어주어야 한다.
while(buffCount < buffSize) {
arr[i++] = buff[buffCount++];
}
}
'문제풀이 > 알고리즘' 카테고리의 다른 글
| [알고리즘] 힙 정렬 ( Heap Sort )이란? (0) | 2021.08.07 |
|---|---|
| [자료구조] 완전이진트리 배열에 저장하기 (0) | 2021.08.06 |
| [알고리즘] 퀵정렬 향상시키기 ( 스택 ) (0) | 2021.08.04 |
| [알고리즘] 퀵 정렬 (Quick Sort)이란? (0) | 2021.08.04 |
| [알고리즘] 버블정렬 향상 시키기 (0) | 2021.08.01 |
