퀵 정렬(Quick Sort)은 이름 그대로
정렬을 빠르게 하는 알고리즘이다.
그러나
버블정렬에 비해 빠를 뿐,
이름만큼 가장 빠른 정렬 알고리즘은 아니다.
퀵 정렬(Quick Sort) 알고리즘이란?
정렬 알고리즘은 두 가지 원칙에서 비롯된다.
1. 두 수의 대소를 비교한다.
2. 두 수의 위치를 교환한다.
'비교' 와 '교환'은 정렬의 근본개념이다. 비교와 교환을 어떻게 하느냐에 따라 다양한 정렬 알고리즘이 만들어진다. 퀵정렬의 비교, 교환 방식을 이해하기 위해 단순한 버블정렬과 비교하여 설명하겠다.

버블정렬은 우측 끝부터 두 수를 비교하는 방식이다. 그래서 포인터가 우측에서 좌측으로 이동하면서 두 수를 비교하여 작은 값을 좌측으로 교환한다.(오름차순)

버블정렬은 동일한 위치에서 비교와 교환이 일어난다. 그러나 퀵정렬은 pLeft와 pRight가 각각 pivot과 비교하고 교환은 pLeft와 pRight에서 일어난다. 즉, 비교와 교환이 분리되어 있다. pLeft는 pivot보다 작은 값을 가리키는 포인터이고 pRight는 pivot보다 큰 값을 가리키는 포인터이다. 원리는 간단하다. pLeft는 pivot다 큰 수를 발견하면 멈추고 pRight는 pivot보다 작은 수를 가리키면 멈춘다. 그 후, 두 값을 '교환'한다.
퀵 정렬 알고리즘 순서
1. pLeft는 우측으로 이동하며 pivot과 하나씩 '비교'한다. 그러다가 pivot보다 크거나 같은 수를 발견하면 멈춘다.
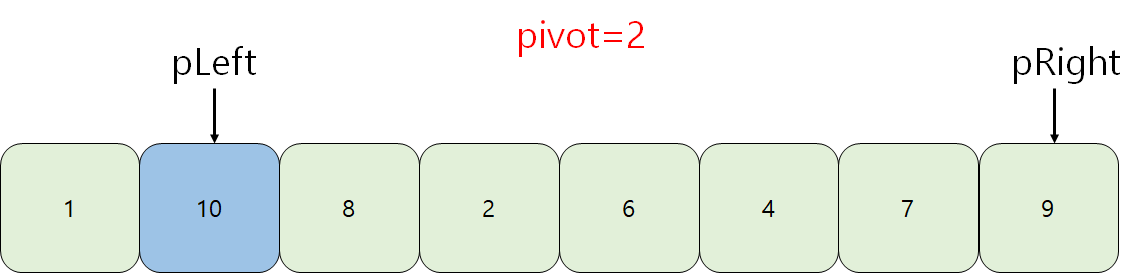
2. pLeft가 멈추면 pRight가 좌측으로 이동하며 pivot과 하나씩 '비교'한다. 그러다가 pivot보다 작거나 같은 수를 발견하면 멈춘다.

3. pLeft가 가리키는 값과 pRight가 가리키는 값을 '교환'한다.
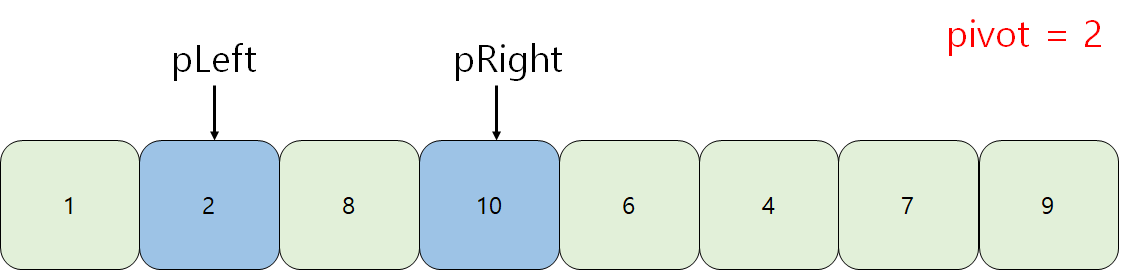
4. 해당 과정을 반복하되 pLeft가 pRight보다 커지면 교환을 중단한다.

5. 좌측끝 ~ pRight 까지는 pivot보다 작은 수로 pLeft ~ 우측끝은 pivot보다 큰 수로 채워진다.

6. 나눠진 구간을 다시 퀵정렬하면 된다. 같은 패턴을 작은 범위로 반복적으로 적용하는 원리이니 '재귀(recursive)'를 사용한다.

7. 좌측끝과 pRight가 겹치거나 우측끝과 pRight가 겹치면 재귀를 중단한다.
코드
public static void quickSort(int left, int right) {
int pLeft = left; // 좌측 끝
int pRight = right; // 우측 끝
int pivot = arr[(left + right)/2]; // pivot
do {
while(arr[pLeft] < pivot) pLeft++; // pivot보다 크거나 같으면 탈출
while(arr[pRight] > pivot) pRight--; // pivot보다 작거나 같으면 탈출
if(pLeft <= pRight) { // pLeft가 pRight보다 작거나 같은 경우만 '교환'
swap(pLeft++,pRight--);
}
}while(pLeft <= pRight); // pRight가 pLeft보다 작아지면 탈출
if(left < pRight) quickSort(left,pRight); //좌측끝 - pRight까지 퀵정렬 재귀호출
if(pLeft < right ) quickSort(pLeft,right); // pLeft - 우측끝까지 퀵정렬 재귀호출
}
//교환
public static void swap(int pLeft, int pRight) {
int tmp = arr[pLeft];
arr[pLeft] = arr[pRight];
arr[pRight] = tmp;
}
정리
이렇듯, 퀵소트는 pivot을 기준으로 구간을 분할하고 재귀(recursive)로 정렬한다. 그러므로 시간복잡도는 재귀가 발생되는 횟수에 따라 결정된다. pivot이 적당히 중간값을 갖는다면 재귀 호출 횟수는 적을 것이다.

그러나 위 그림처럼 pivot이 너무 작거나 큰 값으로 잡히면 구간을 나눈 의미가 무색해진다. 결국 재귀호출의 빈도만 증가하고 시간복잡도만 올라갈뿐이다. 그래서 퀵정렬은 최악의 경우 시간복잡도가 버블정렬과 같은 O(N2)이다. 평균적으로는 O(NlogN)이라 생각하면 된다.
그래서 이름만 '퀵(Quick)'일 뿐, 이름만큼 빠르지 않다. '백준'같은 문제풀이 사이트에서 퀵정렬은 그닥 추천하지 않는다. 알고리즘 문제 풀이는 모든 경우의 수를 테스트한다. 퀵정렬이 최악의 시간복잡도를 가지는 경우도 테스트하므로 시간초과에 걸릴 수 있다. 그러나 일반적으로는 퀵소트가 자주 사용된다고 한다.
'알고리즘 > 알고리즘' 카테고리의 다른 글
| [알고리즘] 합병 정렬 ( Merge Sort )이란? (0) | 2021.08.04 |
|---|---|
| [알고리즘] 퀵정렬 향상시키기 ( 스택 ) (0) | 2021.08.04 |
| [알고리즘] 버블정렬 향상 시키기 (0) | 2021.08.01 |
| [알고리즘] 레드-블랙 트리의 시간복잡도가 O(log n)인 이유 (0) | 2021.06.25 |
| [알고리즘] 보초법(sentinel method)이란? (0) | 2021.06.25 |