힙 정렬( Heap Sort )은
성능 좋은 정렬 알고리즘이지만
원리를 이해하기 쉽지 않다.
그 이유는 완전 이진 트리를
이용하기 때문이다.
[자료구조] 완전이진트리 배열에 저장하기
완전 이진 트리를 이해하기 위해 이진 트리에 대해서 알아보자. 이진 트리란? 위 그림은 이진트리의 가장 기본적인 구조이다. 부모는 자식을 갖는다. 이는 굉장한 의미를 갖는다. 버블정렬, 퀵
lordofkangs.tistory.com
완전이진트리는 위 포스팅에 정리해놓았다.
간단히 요약하면
이진트리는 계층구조에 특별한 조건을 적용하면 탐색효율을 올릴 수 있다. 그 중에서 완전이진트리는 좌측노드부터 빈 노드 없이 채우기에 배열로 구현하기 쉽다. 배열로 구현하려면 부모와 자식간의 인덱스 관계를 알아야 한다. 부모의 인덱스가 N이라면 왼쪽 자식은 2N+1, 오른쪽 자식은 2N+2이다.
정리하면, 부모-자식의 관계에 특별한 조건을 적용함에 따라 다양한 용도의 자료구조가 탄생한다.
대표적으로, 힙(Heap)이 있다.
힙은 완전이진트리에 특별한 조건을 적용한다.
부모의 값은 자식의 값보다 항상 커야한다.
이 조건을 만족하는 완전이진트리를 힙(Heap)이라고 부른다. 이런 조건 덕분에 힙은 최대값과 최솟값을 효율적으로 구할 수 있다. n개의 수를 n번 비교하지 않고 부모-자식 사이만 비교하면 되기 때문이다. 이런 힙의 구조를 이용하여 정렬을 하는 방식을 힙정렬(Heap Sort) 이라 부른다.
힙정렬 ( Heap Sort )
힙정렬은 두 가지 단계로 이루어진다.
1. 힙 만들기
2. 정렬하기
1) 힙 만들기
힙정렬을 위해서는 우선 힙을 만들어야 한다. '부모의 값은 자식의 값보다 항상 커야한다'의 조건을 만족하는 수의 나열을 배열에 저장해야한다. 그러므로 배열의 인덱스는 부모가 N이라면 왼쪽 자식은 2N+1, 오른쪽 자식은 2N+2를 만족해야한다.
우선 수를 배열에 아무렇게나 저장하면 아래와 같은 구조가 된다.

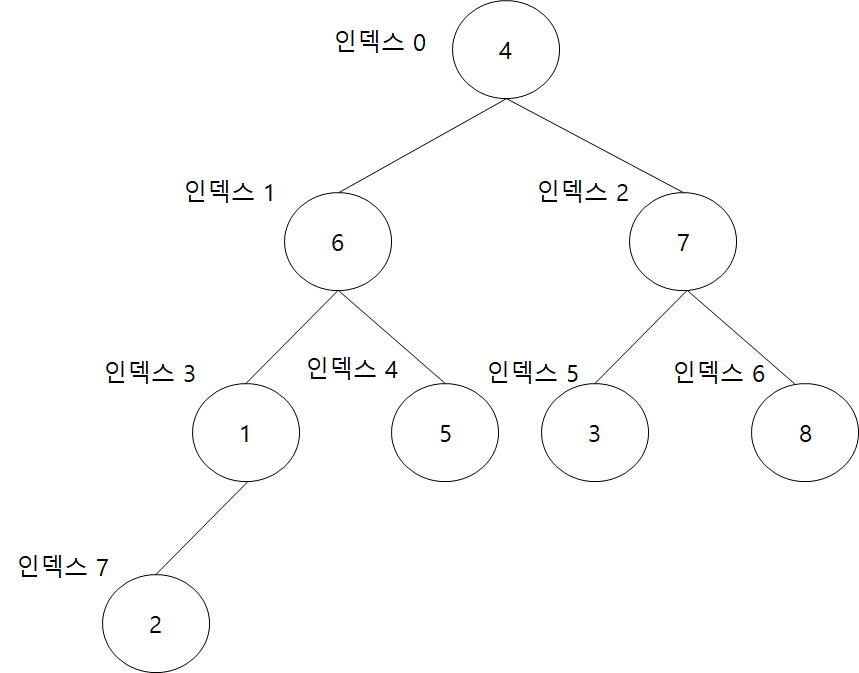
전혀 힙의 조건을 만족하지 않는다. 그러므로 조건에 만족하도록 부모와 자식 간의 대소를 비교하여 위치를 바꾸어주어야 한다.
그럼 어디서부터 비교를 해주어야 할까?
비교는 트리의 가장 아래의 '마지막 부모'부터 시작한다. 한 부모는 다른 노드의 자식일수 있다. 가장 아래 부모가 먼저 대소비교를 해야 그 부모의 부모와 대소비교를 할 수 있다. 그 다음 부모가 또 부모의 부모와 대소비교를 하여 끝으로는 루트와 대소비교를 하여 루트에 최댓값 혹은 최솟값이 오도록 만드는 원리다. 토너먼트 방식과 같다.
그렇다면 가장 아래에 위치한 마지막 부모의 인덱스를 구해보자. 원리는 간단하다.
가장 마지막 자식의 부모가 가장 마지막 부모이다.
배열의 크기 : 8
가장 끝 인덱스 : 7
그러므로, 인덱스 7의 부모가 힙의 마지막 부모이다.
부모의 인덱스가 N이라면 왼쪽 자식은 2N+1, 오른쪽 자식은 2N+2이다. 그러므로 자식의 인덱스가 M이라면 부모의 인덱스는 ( M - 1 ) / 2이다. 오른쪽 자식은 M-1을 하면 홀수이므로 2로 나누면 소수점이 나온다. 그러나 인덱스는 정수이기에 정수 자료형에 저장할 것이다. 그러면 자연스레 캐스팅이 이루어져 소수점이 없어진다.
고로 자식인덱스가 M일때 , ( M - 1 ) / 2가 부모 인덱스가 된다.

( 7 - 1 ) / 2는 3이므로 인덱스 7의 부모는 인덱스 3이다. 그러므로 가장 마지막 부모보다 작은 인덱스는 모두 부모가 된다. 인덱스 3, 인덱스 2, 인덱스 1, 인덱스 0의 노드가 자식을 가진 부모이다.
부모와 자식의 대소관계를 비교하는 알고리즘을 F(N)이라고 하자.
인덱스 N이 3부터 0이 될 때까지 알고리즘 F(N)을 토너먼트같이 반복하면 배열은 힙(Heap) 자료구조가 된다.
2) 정렬하기
모든 정렬 알고리즘은 두 가지 원칙에서 비롯된다.
1. 두 수의 대소를 비교한다.
2. 두 수의 위치를 교환한다.
'비교' 와 '교환'은 정렬의 근본개념이다.
2-1) 힙정렬의 교환
힙생성이 끝나면 부모가 자식보다 항상 큰 배열이 완성된다. 그럼 이제 오름차순 정렬을 만들 차례이다. 배열의 가장 큰 값은 루트에 있다. 위 배열에서는 10이 가장 큰 수이다. 그리고 힙의 루트인 인덱스0에 자리잡는다. 오름차순은 작은 값에서 큰 값으로 정렬하는 것이므로 루트와 우측 끝의 위치를 바꾸어준다. 그럼 10(root)는 가장 우측으로 가고 루트자리는 1이 온다.
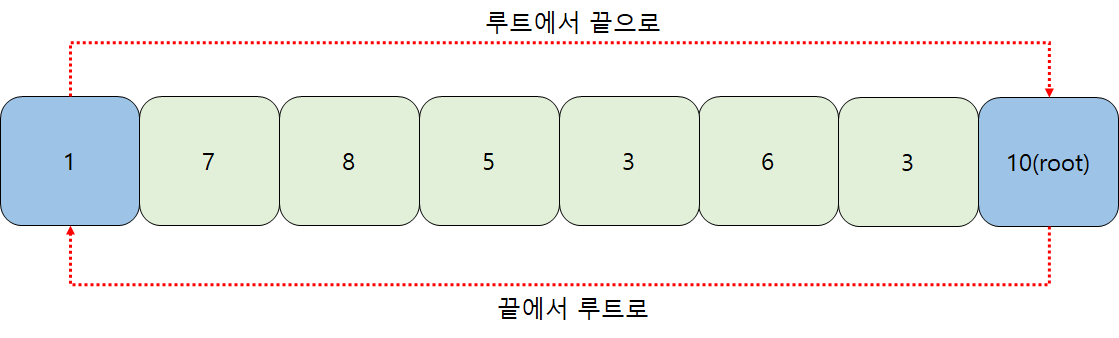
가장 큰 값이 가장 끝으로 갔다. index가 7인 자리에 가장 큰 값이 갔으므로 7은 정렬되었다. 이제 0-6까지 정렬해야한다. 다시 힙정렬을 하면 루트자리에 가장 큰 값이온다. 그럼 이를 index 6자리로 보내고 다시 힙정렬을 한다. 위 과정을 반복하면 오름차순 정렬이 완료된다.
2-2) 힙정렬의 비교
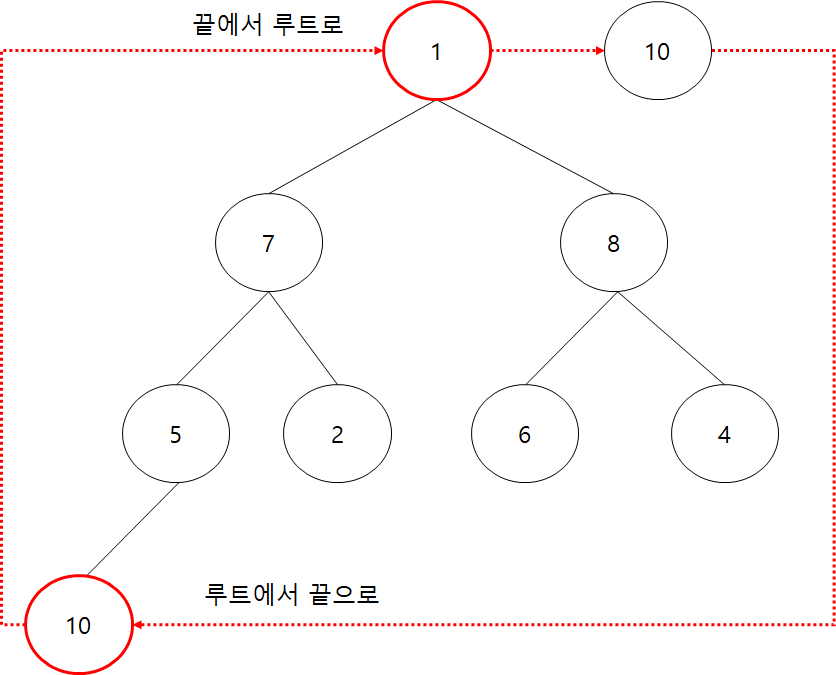
루트를 가장 끝으로 보냈으니 남은 수 가운데에서 최대값을 다시 산출해야한다. 10을 제외하고 남은 수들로 다시 힙 알고리즘을 돌려 힙을 만들어 준다. 가장 작은 값이 루트가 되었으므로 비교는 모든 부모 자식 사이에서 일어난다. 그렇게 힙알고리즘을 통해 부모와 자식을 비교하여 가장 큰 값을 위로 올린다. 이것이 힙정렬의 비교이다.
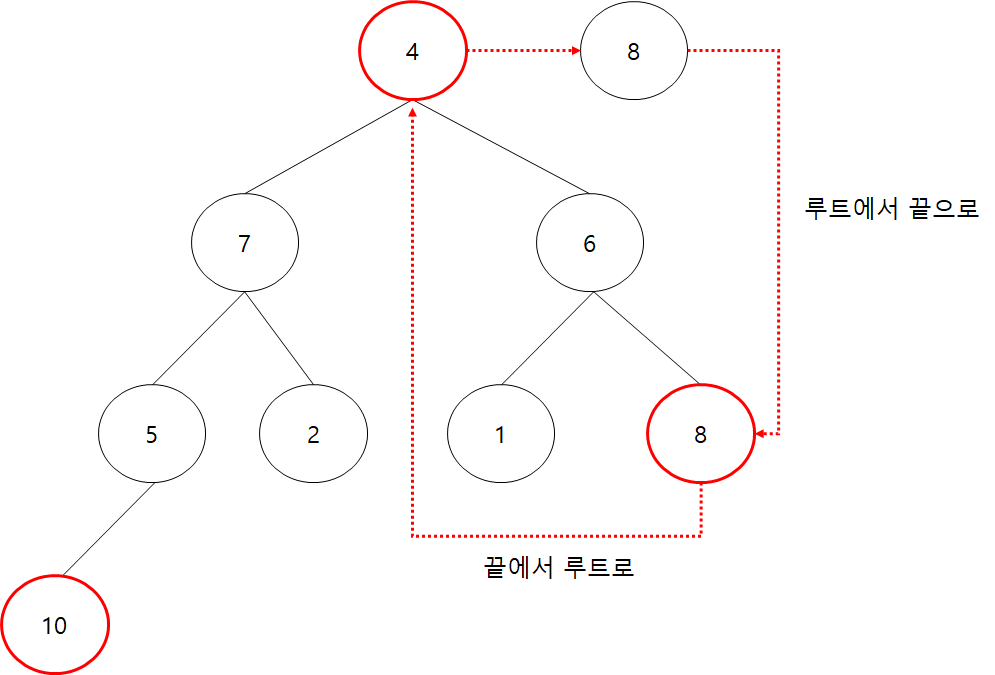
힙 알고리즘의 비교와 루트와 가장 끝 노드를 교환하는 방식을 반복하면 오름차순 정렬이 완성된다.
코드
public static void doHeapSort() {
int lastIndex = arr.length - 1;
int lastParent = ( lastIndex - 1 ) / 2;
// 1) 힙 만들기
for( int i = lastParent; i >= 0; i--) {
doHeap(i,lastIndex);
}
// 2) 정렬하기
for( int i = lastIndex; i>0; i--) {
swap(0,i); // 0이랑 가장 끝 교환하기
doHeap(0,i-1);
}
}
public static void doHeap(int value, int lastIndex) {
int pivot = arr[value];
int parent;
int child = 0;
for( parent = value; parent <= (double)(lastIndex - 1)/2; parent = child) {
int leftChild = 2*parent + 1;
int rightChild = leftChild + 1;
if( rightChild > lastIndex) child = leftChild;
else {
child = arr[leftChild] > arr[rightChild] ? leftChild : rightChild;
}
if(pivot >= arr[child])break;
else {
arr[parent] = arr[child];
}
}
arr[parent] = pivot;
}
public static void swap(int value1, int value2) {
int tmp = arr[value1];
arr[value1] = arr[value2];
arr[value2] = tmp;
}'문제풀이 > 알고리즘' 카테고리의 다른 글
| Greedy 예제(2) Min Deletion Cost (0) | 2021.10.29 |
|---|---|
| Greedy 예제(1) 트럭에 물건 많이 채우기 (0) | 2021.10.29 |
| [자료구조] 완전이진트리 배열에 저장하기 (0) | 2021.08.06 |
| [알고리즘] 합병 정렬 ( Merge Sort )이란? (0) | 2021.08.04 |
| [알고리즘] 퀵정렬 향상시키기 ( 스택 ) (0) | 2021.08.04 |
