[인공지능] 지식표현방법 ( 명제논리, 술어논리 )
명제논리 참 또는 거짓을 판별 할 수 있는 문장 P : 마트는 월요일부터 토요일까지 영업한다. ( 지식 ) Q : 오늘은 월요일이다. ( 사실 ) R : 마트는 오늘 영업한다. ( 추론된 사실 ) 새로운 '사실'을
lordofkangs.tistory.com
명제는 참 또는 거짓으로 표현하지만
실제 세계는 그렇지 않다.
인간은 모호한(fuzzy) 표현을 자주 사용한다.
퍼지 논리란,
모호한 표현을 명확하게 표현하는 방법이다.
명제 논리
- 키가 크다. ( 1 )
- 키가 작다. ( 0 )
퍼지 논리
- 키가 매우 큼 ( 1.0 )
- 키가 큼 ( 0.8 )
- 키가 약간 큼 ( 0.6 )
- 키가 작음 ( 0.0 )
퍼지 논리는 '참'과 '거짓'이 아닌 '소속도'로 나타낸다.
크리스프 집합
기존의 집합이론
소속하면 '1' (True)
소속하지 않으면 '0' (False)
키가 큰 사람 집합에 소속된 키 = 181, 188, 190
키가 큰 사람 집합에 소속되지 못한 키 = 170, 161
퍼지 집합
소속된 함수값을 0과 1 사이의 값으로 대응
키 큰 사람 집합 A : { 172cm, 175cm, 185cm, 190cm }

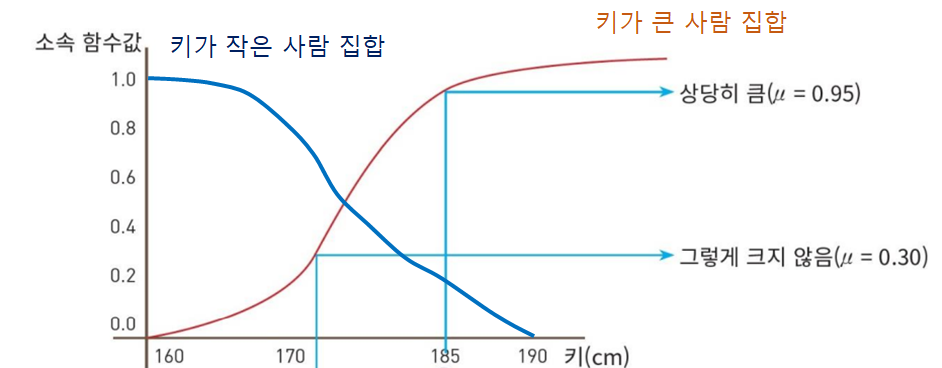
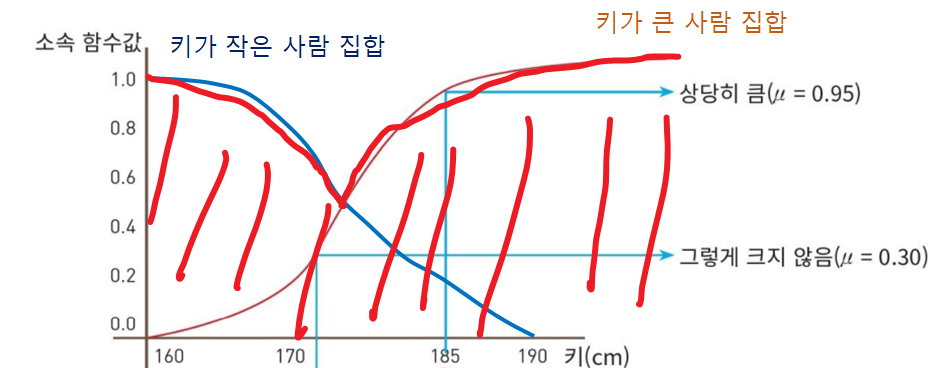
키 172는 집합 A에 0.3 정도 소속됨
키 175는 집합 A에 0.5 정도 소속됨
키 185는 집합 A에 0.95 정도 소속됨
키 190은 집합 A에 완전 소속(1.0) 됨
키 큰 사람 집합 A : { 0.3/172cm, 0.5/175cm, 0.95/185cm, 1.0/190cm }
퍼지집합의 연산자
교집합과 합집합은 두 개의 집합의 연산이다.
동일한 x에 대하여 두 개의 서로 다른 함수가 존재할 때
교집합은 소속도가 낮은 함수를 선택하고
합집합은 소속도가 높은 함수를 선택한다.
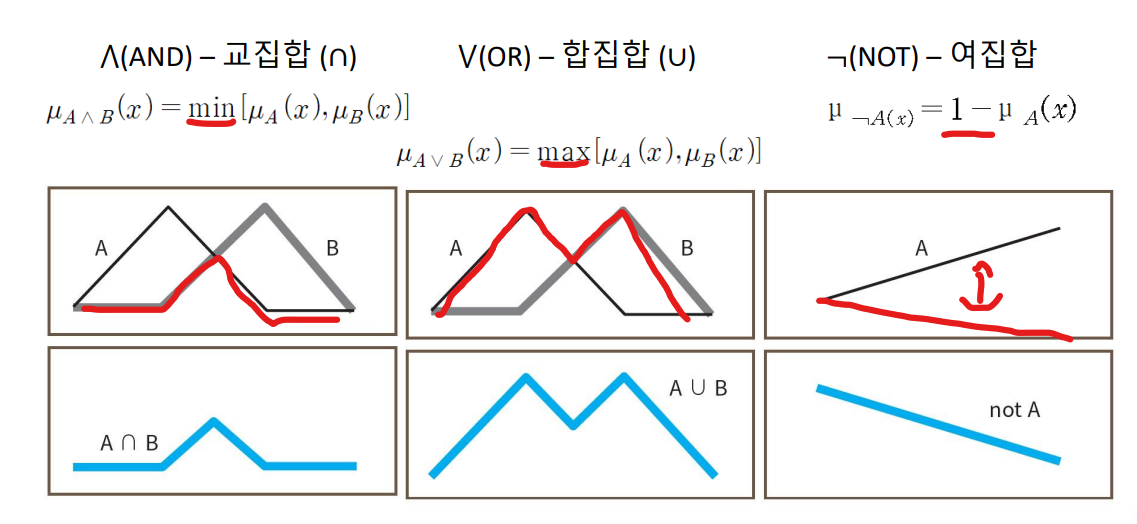
EX)
1) 키가 작으면서 키가 큰 사람 집합 ( 키가 어중간한 사람들 )
교집합이므로 두 함수를 비교하여 소속도가 최소(min)인 함수를 구한다.

키가 완전 작거나 키가 완전 크면 소속도가 작다. 가장 중간 키가 교집합의 소속도가 가장 높다.
2) 키가 작거나 키가 큰 사람의 집합 ( 키가 완전 작거나 완전 큰 사람들 )
합집합이므로 두 함수를 비교하여 소속도가 최대(max)인 함수를 구한다.
키가 완전 작거나 키가 완전 커야 소속도가 가장 높다. 키가 어중간하면 소속도가 가장 작다.
집중화 연산자 ( CONcentration ) 와 팽창 연산자 ( DILation )
인간은 '매우', '약간' 이라는 모호한 표현을 사용한다.
퍼지논리는 이를 명확하게 표현한다.
- 집중화 연산자 ( CONcentration )
'매우'라는 표현이 들어가면 소속도에 '제곱'을 해준다. 소속도는 1보다 작으므로 제곱을 하면 값이 작아진다. 이때 소속도가 0에 가까울수록 작아지는 비율이 커진다. 고로 집중화 연산은 작은 소속도를 더 작게 만드는 연산이다.

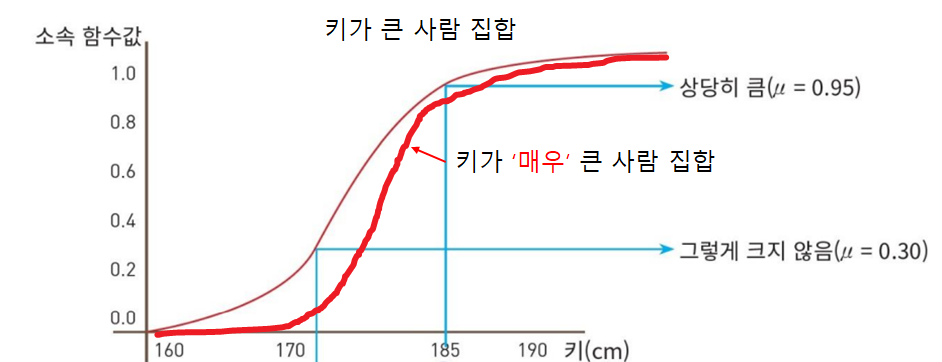
| 키가 큰 사람 | 키가 '매우' 큰 사람 |
| 0.3/170 | 0.09/170 |
| 0.50/175 | 0.25/175 |
| 0.95/180 | 0.90/180 |
| 1.0/190 | 1.0/190 |
- 팽창 연산자 ( DILation )
'약간'이라는 표현이 들어가면 소속도의 '제곱근'을 구한다. 소속도는 1보다 작기에 루트를 씌우면 값이 더 커진다. 소속도가 0에 가까울수록 값이 크게 증가한다. 고로, 팽창 연산자는 작은 소속도를 더 크게 만드는 연산이다.


| 키가 큰 사람 | 키가 '약간' 큰 사람 |
| 0.3/170 | 0.55/170 |
| 0.50/175 | 0.70/175 |
| 0.95/180 | 0.97/180 |
| 1.0/190 | 1.0/190 |
퍼지 추론 ( 역퍼지화 )
추론 : 전제 → 결론
전제 : 퍼지집합 A → 소속도 ( 퍼지화; Fuzzification )
결론 : 소속도 → 퍼지집합 B ( 역퍼지화; Defuzzification )

온도에 따라 팬의 속도를 조절하는 간단한 인공지능이 구현되었다.
전제가 여러가지인 경우 ( Max-Min 추론 )
전제 : Max 연산
결론 : Min 연산
전제1 : 온도가 높다. ( 0.1 )
전제2 : 습도가 높다. ( 0.7 )
전제가 다수인 경우, 여러 전제의 소속도를 비교하여 Max 소속도를 구한다.
소속도(0.7) = max ( 0.1 , 0.7 )
전제를 통해 소속도를 구했으니 이제 역퍼지화해야한다.

전제의 소속도는 Max 소속도로 최상의 경우이다. 그러므로 Max 소속도로 산출되는 퍼지집합보다 작은 소속도(Min)로 역퍼지화하여 퍼지집합(에어컨 세기)을 구한다.
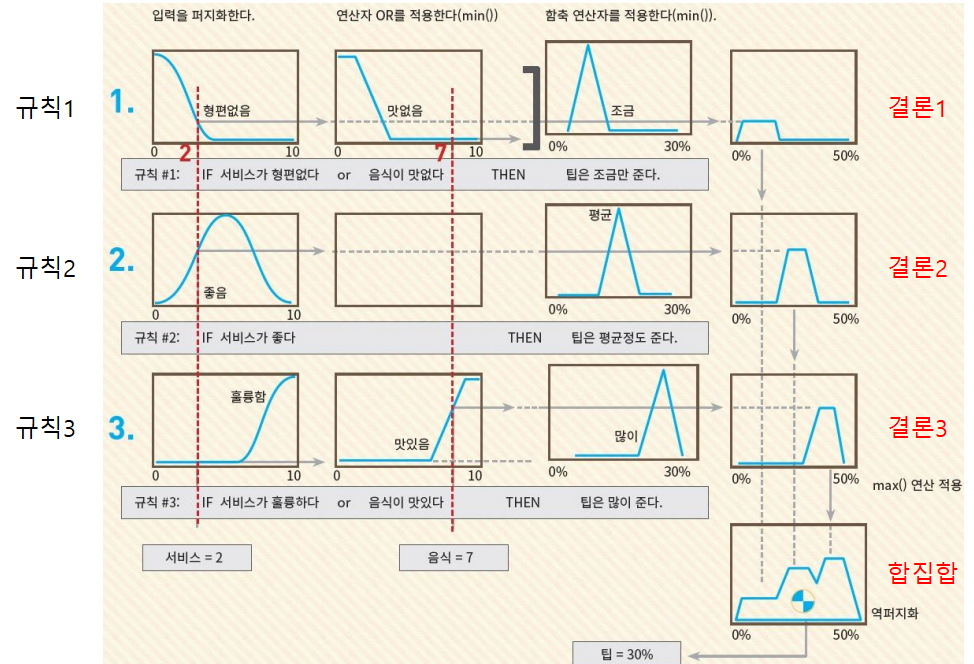
규칙이 다수인 경우
규칙이 여러 개면 결론도 여러 개다. 하나의 규칙은 Max-Min 추론을 통해 역퍼지화하여 퍼지집합을 구한다. 결론이 여러 개이므로 역퍼지화 된 퍼지집합도 여러 개이다. 모든 규칙을 고려해야하므로 퍼지집합 그래프를 합집합 한다.
'CS > 인공지능' 카테고리의 다른 글
| [인공지능] 베이즈 정리 ( Bayes' theorem ) (0) | 2021.11.02 |
|---|---|
| [인공지능] 조건부 확률 (0) | 2021.11.01 |
| [인공지능] 지식표현방법 ( 명제논리, 술어논리 ) (0) | 2021.10.30 |
| [인공지능] 지식표현방법 ( 의미망, 프레임 ) (0) | 2021.10.30 |
| [인공지능] 전문가시스템 (0) | 2021.10.29 |
