L.O.K

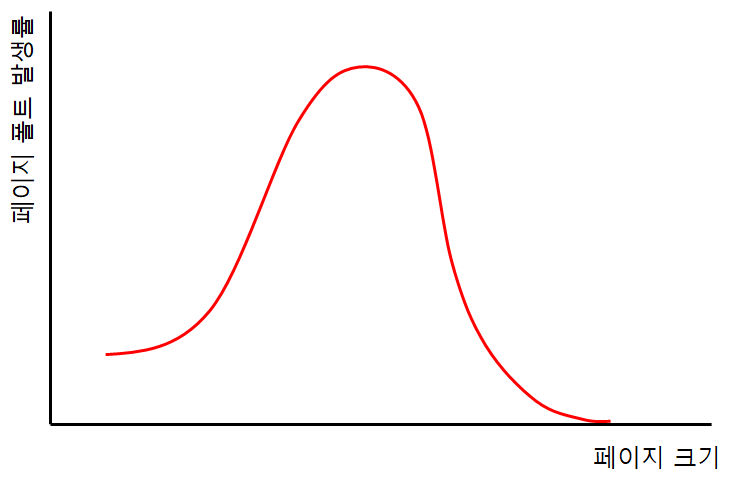
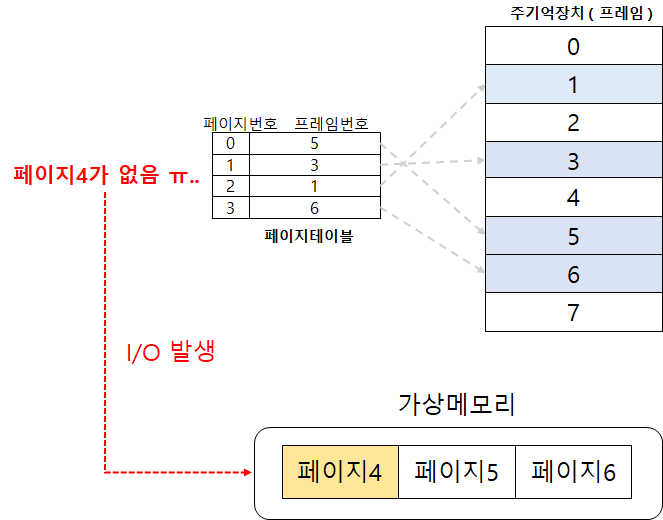
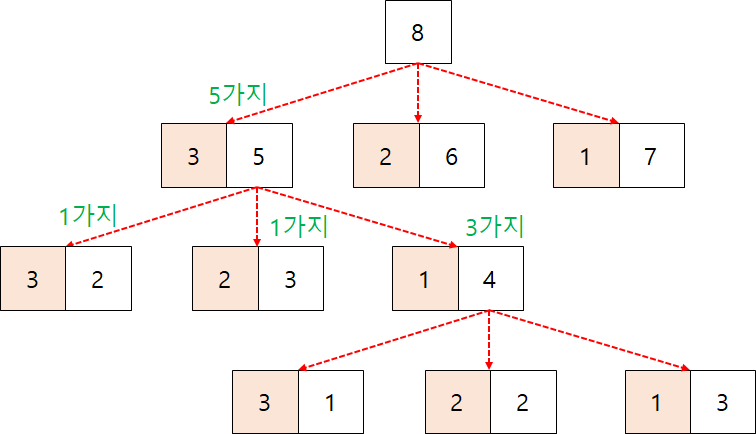
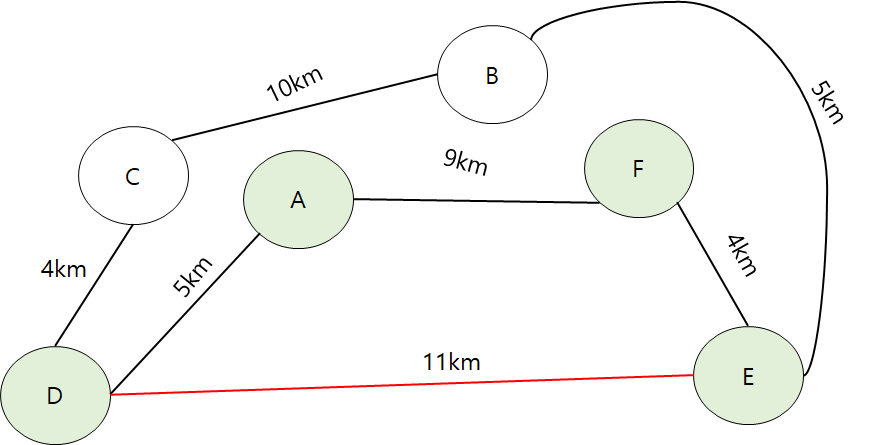
페이지 크기는 하드웨어 설계의 중요한 요소이다. 페이지 크기가 많은 요소에 영향을 끼친다. 1. 페이지 테이블 크기 2. 프레임 내부 단편화 3. 참조지역성 효과 4. 입출력 시간 효율성 1. 페이지 테이블 크기 지난 포스팅에서 구체적으로 다루어 보았다. [운영체제] 가상메모리와 페이징 기법 [운영체제] 가상메모리 기법 [운영체제] 메모리 분할 ( Memory Partioning ) [ 비연속 메모리 할당 ] [운영체제] 메모리 분할 ( Memory Partioning ) [ 연속 메모리 할당 ] 다수의 프로세스에게 메모리를 분할해 lordofkangs.tistory.com 2. 프레임 내부 단편화 페이지를 크게 나누면 프로세스 블록이 페이지를 모두 채우지 못하는 내부단편화가 발생할 수 있다. 내부단편화..

가상 메모리 기법은 메모리 참조시, 논리주소를 동적으로 물리주소로 변환하여 참조한다. 최소 두 번의 참조가 발생한다. 1) 페이지 테이블 참조 2) 실기억장치 참조 두 번의 참조는 두 배의 메모리 접근 시간이 걸리도록 만든다. 이 문제를 해결하기 위해 TLB( Tranlation Lookaside Buffer) 즉, 고속 캐시를 사용한다. TLB TLB는 고속 캐시이다. 즉, 하드웨어다. TLB는 병렬판독회로(하드웨어)가 있어 원하는 페이지를 단번에 찾을 수 있다. 이를 연관사상이라 한다. 굉장히 빠르다. 가장 최근에 참조된 페이지를 TLB에 저장한다. 특정 페이지가 필요 시, 먼저 TLB를 검사한다. 적중(HIT)하면 바로 물리주소로 변환하여 주기억장치에 접근한다. 적중(HIT)하지 않으면 OS는 페이..

[운영체제] 메모리 분할 ( Memory Partioning ) [ 비연속 메모리 할당 ] [운영체제] 메모리 분할 ( Memory Partioning ) [ 연속 메모리 할당 ] 다수의 프로세스에게 메모리를 분할해줘야 한다. 이번 포스팅에서는 연속 메모리 할당 방식의 메모리 분할법을 다루겠다. 연속 메 lordofkangs.tistory.com 지난 포스팅에서 프로세스를 주기억장치에 할당하는 방법을 다루었다. 프로세스 전부를 주기억장치에 할당하면 메모리를 효율적으로 사용할 수 없다. 만약 두 가지 조건을 만족하면 필요하지 않은 블록은 보조기억장치로 보낼 수 있다. 가상메모리 기법 운용 조건 1) 프로세스의 메모리 참조는 논리주소로 이루어지고 동적으로 물리주소로 변환된다. 물리주소는 실제 블록이 메모리에..

예제) 어떤 퀴즈대회에서 숫자게임이 진행되었다. 숫자게임의 규칙은 주어진 범위 안의 숫자들을 더해 목표하는 수를 만드는 것이다. 중복된 숫자를 사용하는 것은 가능하지만 숫자들의 조합은 두 사람 이상 똑같이 사용할 수 없다. 사용 가능한 숫자 범위와 목표하는 수가 주어졌을 때, 목표하는 수를 만들 수 있는 최대 경우의 수를 구하시오. 숫자 범위 [ 1 , 2 , 3 ] 목표 : 8 ( 답지에 답은 10이라 나온다. 근데 문제 조건이 너무 헷갈리고 'SSAFY 5일완성' 책이 오류가 상당히 많다. 조건이 애매하니 어떻게 해석하느냐에 따라 결과가 달라진다고 생각한다. 그래서 그냥 내가 해석한 방식대로 풀었고 답은 31은 나왔다. ) 1, 2, 3을 더해 8을 만드는 경우의 수를 구하는 문제이다. 동적계획법의 ..

예제) 남자 m명과 여자 n명이 있다. 남자는 여자보다 많고 커플은 여자의 수만큼 생성된다. 여자는 키가 큰 순서로 선택할 수 있다. 남자는 키 순서대로 서있다. 한 여자가 한 남자를 선택했을 때, 다음 여자는 선택된 남자보다 키 큰 남자를 선택할 수 없다. 남성의 키가 모두 다를 때, 커플이 탄생할 수 있는 경우의 수를 구하라. ( 개인적으로 이게 뭔 문제인지 감도 잘 안 잡혔다. 동적계획법에 억지로 문제를 끼어맞추다보니 이상한 문제가 탄생한거 같다. 그래도 한 번 풀어보자. ) 결국 커플은 n개 탄생한다. 동적계획법을 발상하려면 두 가지를 고려하면 된다. 1) 큰 단위와 작은 단위에 공통으로 적용되는 원리를 발견한다. 2) 큰 단위와 작은 단위를 분리한다. 첫 번째 여자는 3명의 남자를 선택할 수 있..

예제 ) 하노이탑 원반의 개수가 주어질 때 원반을 이동시킬 최소 횟수를 구하시오. 규칙 1. 1회에 한 개의 원판만 옮길 수 있다. 2. 반드시 큰 원판 위에 작은 원판이 있어야 한다. . 1번에 쌓여있는 원판들을 규칙을 지키며 3번까지 옮겨야 한다. 동적계획법의 TopDown 방식에 따라 결과부터 생각해보자. n개의 원판을 3번 막대로 옮기려면 우선, n-1개 원판을 2번 막대로 옮겨야 한다. 그래야 가장 큰 원판을 3번으로 옮길 수 있다. 그 다음, 2번 막대의 n-1개 원판을 다시 3번 막대로 옮긴다. 공식으로 나타내보자. n : 원판 갯수 F(n) : n개의 원판을 한 막대에서 다른 막대로 옮기는 경우의 최소 횟수 과정 1) n-1개 원판을 1번에서 3번으로 이동 : F(n-1) 2) 가장 큰 원..

예제) 철수는 매일 점심마다 짜장면이나 짬뽕을 먹는다. 시험기간이 n일 남았을 때, 철수가 짜장, 짬뽕을 먹는 경우의 수를 구하라. ( 단, 짜장면은 2일, 4일, 6일... 같이 짝수날을 연속으로 먹어야 한다. 또한 짜장면을 먹고 짬뽕을 먹은 뒤 다시 짜장면을 먹을 수 없다. ) 조건이 까다롭다. 조건1) 짜장면은 2, 4, 6... 연속으로 먹을 수 있다. 조건2) 짜 → 짬 → 짜 순으로 먹을 수 없다. 경우의 수를 따질 때, 동적계획법으로 접근하면 효율적이다. 시험기간 n일을 작은 단위로 분류해야한다. 조건1)은 분류에 적합하다. 예를들어, 시험기간이 8일이 남았다고 해보자. 1) 짜장면을 8일 먹은 날 2) 짜장면을 6일 먹은 날 3) 짜장면을 4일 먹은 날 4) 짜장면을 2일 먹은 날 5) 짜..

예제 ) 시작도시와 목표도시가 주어질 때, 목표도시까지 가는 최단 경로를 구하시오 시작도시 : A 목표도시 : E 다익스트라 알고리즘을 사용한다. 각 노드마다 접근된 경로의 길이를 기록한다. 최단 경로이므로 최소길이만 기록한다. D노드와 C노드와 F노드는 다음과 같은 접근 경우를 가질 수 있다. 경우 중 최소를 제외한 나머지는 제거한다. 이런 방식으로 각 노드의 최단 경로 길이를 구한다. 최소만 남긴다. 마지막으로 목표노드의 최단 경로 길이를 구해보자. A에서 E까지 최단경로길이는 17km이다. 참고자료 2021년 7기 모집대비 SSAFY(삼성 청년 SW아카데미) SW적성진단 5일 완성 ㆍ객관식 이론 + 대표유형 + 유형 + 고난도 문항 수록ㆍ주관식 대표유형 + 유형 + 고난도 문항 수록ㆍ객관식 & 주관..

예제) 모든 도시를 오갈 수 있는 고속도로를 건설하려고 할 때, 총 고속도로 길이의 최소값을 구하라. 복잡하다. 써클(Circle)이 보이도록 만들어보자. 써클이란, 지점들이 서로 연결되어 순환하는 구조를 말한다. 최소길이의 고속도로를 만들려면 고속도로가 최소 개수여야 한다. n개의 지점이 있으면 n-1개의 길만 있으면 된다. 이를 최소신장트리(Spanning Tree)라고 한다. 최소신장트리를 만들려면 순환구조를 없애야 한다. 최대길이의 간선을 제거하여 총 길이가 최소 길이인 스패닝트리를 만드는 것이 목적이다. 1) D - F - E 써클 D와 F를 잇는 간선이 12km로 가장 길다. 고로 제거한다. 총 제거 길이 : 12 2) D - A - F - E 써클 D-F를 제거했더니 또 다른 써클이 생성되었..

예제) 주어진 문자열을 수정하여 하나의 문자로만 구성된 문자열을 만드려고 할 때, 최소로 수행되는 수정 횟수를 구하시오. ( 연속적인 문자는 하나의 문자로 통일 가능하다. ) AABACCBABA 위 문자열을 AAAAAAAAAA 나 BBBBBBBBBB나 CCCCCCCCCC로 바꾸라는 말이다. 수정횟수를 최소로 하려면 가장 자주 등장하는 문자를 제외한 나머지 문자를 수정해야한다. ( Greedy 알고리즘 ) 알고리즘 1) 포인터로 문자열을 검사해서 문자별 등장횟수를 카운트한다. 2) 동일한 문자가 연속되면 카운트하지 않는다. 3) 등장 횟수가 많은 문자를 제외한 두 문자의 등장횟수 합이 최소 수정횟수이다. A가 등장했다. 현재 문자는 A로 입력되고 A 등장횟수는 1 올라간다. A가 연속해서 등장했다. 현재문..